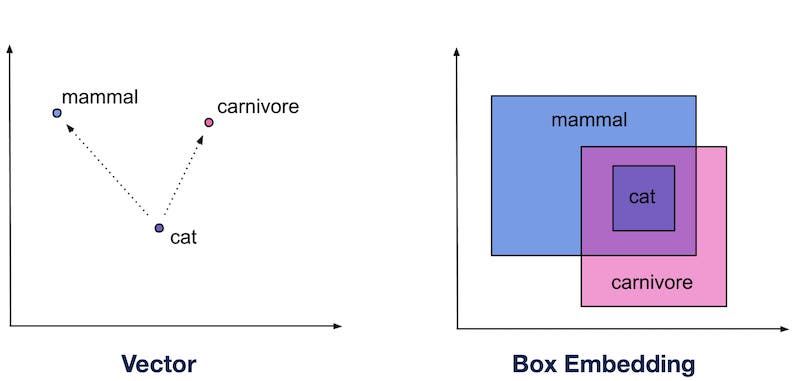
自然言語処理を中心に、データをベクトルで表現する埋め込み表現は、深層学習の基礎的な技術として盛んに研究されています。しかしながら、埋め込み表現はデータをベクトルとして表現するため、必然的にすべてのデータが点として扱われることとなります。一方で現実世界の事物には、多種多様・複雑な階層構造が潜在的に存在します。例えば、「犬」という概念は「動物」よりも下位の概念であり、「犬」と「猫」は並列的な概念であると言えるでしょう。
既存の埋め込み表現は、このような階層構造をうまく捉えることができませんでした。データを「点」以外の形式で表現する手法として、以前 Box Embedding と呼ばれる、データを「箱」で表現する手法を紹介しました (解説記事) が、ベクトルのまま、このような階層構造をうまく捉える方法は存在しないのでしょうか。
本記事では、歪んだ空間である双曲空間上のベクトルとしてデータを埋め込む手法である 双曲埋め込み (Hyperbolic Embeddings) を紹介します。まず、双曲埋め込みの代表的な手法である Poincaré Embeddings について周辺技術から解説し、さらに双曲埋め込みの発展的・応用的な手法について解説します。そして最後に、双曲埋め込みと強化学習を組み合わせ、強化学習における状態と行動の階層関係を暗黙的に学習する最新の手法についても紹介します。
文責:塚越 駿(名古屋大学)
ステート・オブ・AI ガイドでは、人工知能・機械学習分野の最新動向についての高品質な記事を毎月5〜6本配信しています。購読などの詳細につきましては、こちらをご覧ください。また、Twitter アカウントの方でも情報を発信しています。
双曲埋め込みの概要
双曲埋め込みについて解説する前に、まずは双曲埋め込みを支える事前知識についてみていきます。私たちは普段、ユークリッド空間と呼ばれる、平坦な空間に生きています。
それに対し、本記事で扱う双曲空間 (hyperbolic space) とは、平坦ではない、曲がった空間の一種です。このような曲がった空間には、実はさまざまなものを考えることができ、平坦なユークリッド空間を含むこれらを総称して多様体と呼びます。
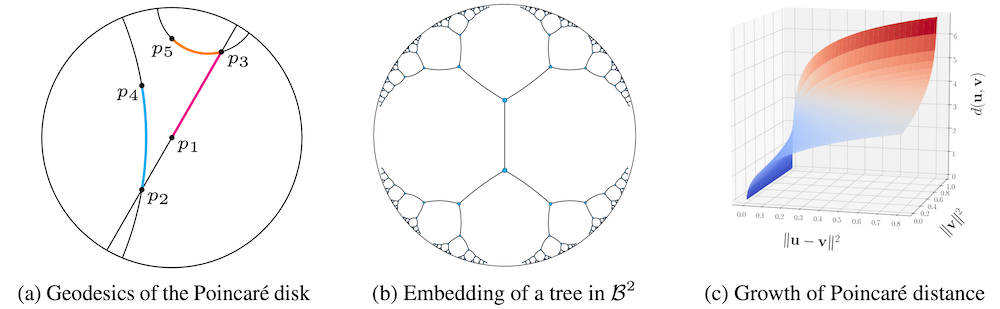
代表的な多様体のイメージ図を見てましょう。図は Gu et al., 2019 からの引用です。
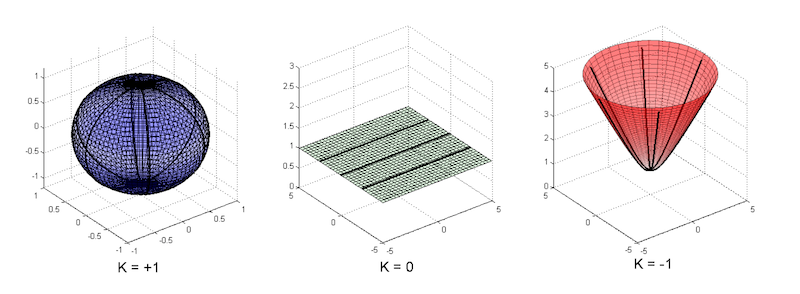
左の図形は、2次元超球平面を表しています。2次元超球平面は「3次元空間の中にある球の表面」であるというのが直感的な理解です。
具体的なイメージとして、私たちが普段住んでいる地球の表面を想像してみてください。例えば、地球上を真っ直ぐ、直線的に歩いて世界一周することを考えます。このとき、私たちが歩く経路は、真っ直ぐに歩くので地球の表面から見れば間違いなく直線のはずですが、宇宙空間から見ればその経路は円を描いています。このように、球の表面だけを考えるのが超球平面です。
中心の図形は、2次元ユークリッド空間 (平面) を表しています。私たちがよく考えている2次元平面は、このような形状をしていますね。
右の図形が、本記事で扱う2次元双曲空間 (平面) です。双曲空間は、原点から遠ざかるほど、空間が広くなるような性質を持っています。この性質が、木構造などの階層構造を表現するのに適しており、近年木構造をはじめとしたさまざまなネットワーク構造をうまく表現するために注目されているというわけです。
歪んだ空間では、距離の測り方が変化します。例えば、地球上で日本からアメリカに行こうとする場合、3次元球としての地球を考えると、日本からアメリカまで直線的な穴を掘って移動するのが最短経路になります。しかし、地球平面という2次元球面での移動を考えるなら、地球表面に沿って移動する必要があります。このような事情から、歪んだ空間で何らかの距離を測りたい場合は、空間の曲がり方にしたがって距離を測ってあげる必要があります。
そのことを図示したのが、上述の各空間上に3角形を描いた以下の図です。図は Gu et al., 2019 からの引用です。
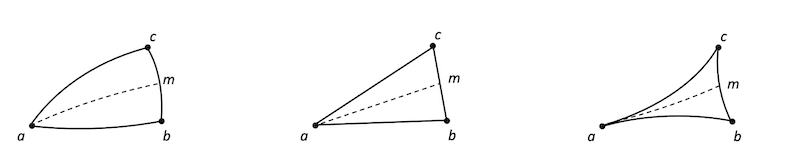
左の超球平面上の三角形は、球面に合わせて距離を測るので、三角形の辺が膨らんでいます。中心のユークリッド空間上の三角形は、私たちが普段扱う、平坦な三角形ですね。右の双曲平面上の三角形は、超球平面とは逆に、凹んだ三角形をしています。
このように、双曲空間は歪んだ空間です。したがって、通常のユークリッド空間で素直に表現することはできません。そのため、双曲空間をユークリッド空間で表現する方法がいくつか提案されてきました。
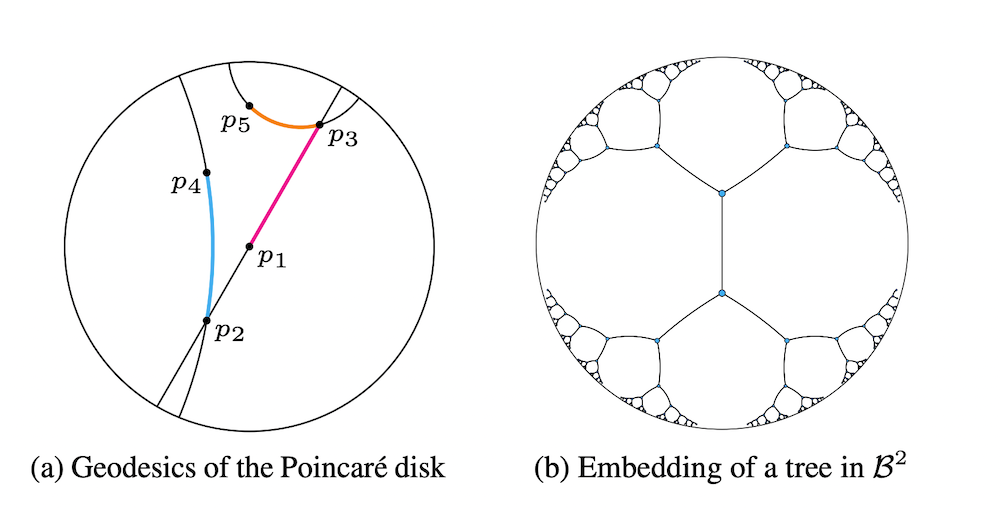
その中でも代表的なものが、本記事で主に解説する Poincaré Embeddings が採用している表現方法であるポワンカレ球 (Poincaré ball) です。
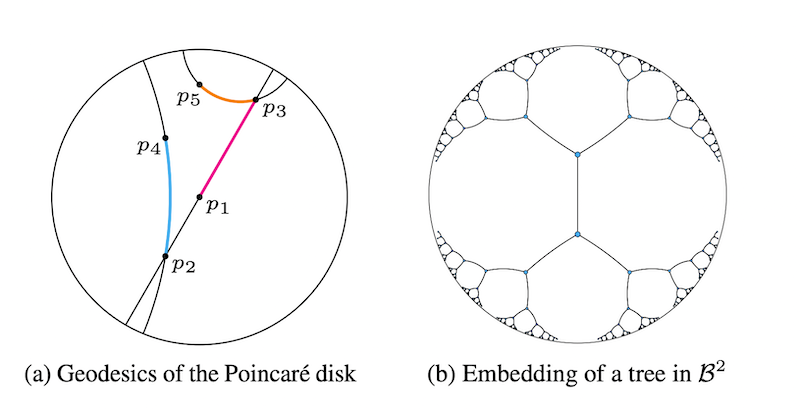
ポワンカレ球は、半径1の球の範囲内で、双曲空間を表現します。ポワンカレ球ではこの球の外側にいくほど、空間が広くなっていきます。これは、無限に広がっていく双曲空間を、半径1の球という狭い範囲に押し込んだことによる効果です。
データを空間に埋め込むことを考えた時、ポワンカレ球では外側にいくほど細かく繊細に情報を埋め込むことができ、逆に中心近くには荒めに情報が埋め込まれるということです。そのことを表現したのが上の図の右側の、ポワンカレ球上の木を表現した図です。
双曲空間のモデルについて理解を深めるには、下記の双曲空間での移動を可視化したブログ記事が非常に参考になります。
それでは、前置きが長くなりましたが、双曲空間にデータを埋め込むにはどうすればよいかについてみていきましょう。
双曲埋め込み
Poincaré Embeddings
元論文: Nickel et al., NIPS 2017. Poincaré Embeddings for Learning Hierarchical Representations
GitHub: https://github.com/facebookresearch/poincare-embeddings
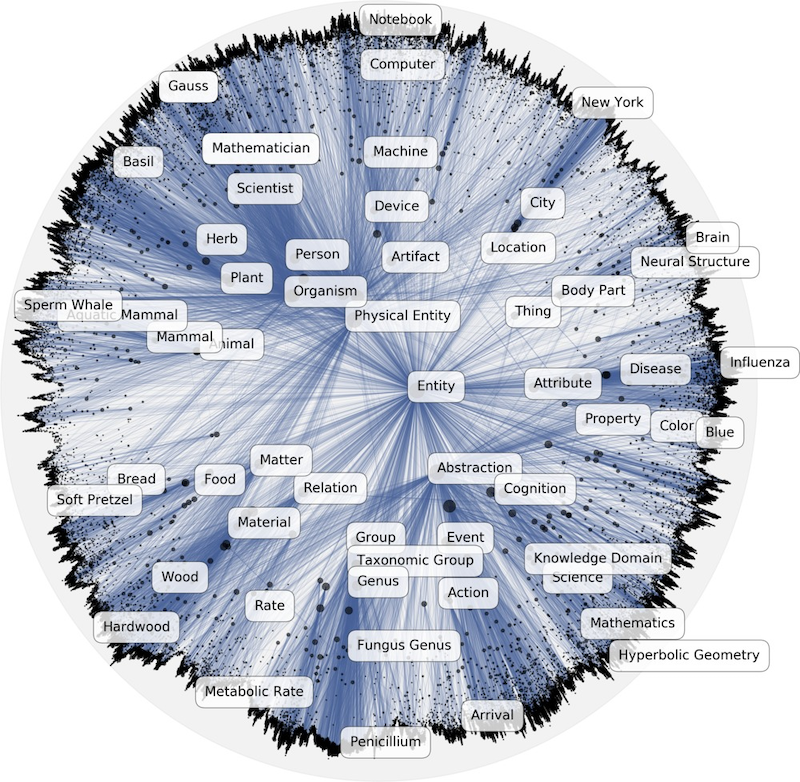
Nickel らによって提案された Poincaré Embeddings は、データを双曲空間に埋め込むことで、データ同士の階層関係を捉えた表現を学習するという手法です。
Poincaré Embeddings は、低次元の埋め込み表現でも適切に階層関係の表現ができます。具体的には、ユークリッド空間に単語を埋め込む既存手法である、Word2Vec を用いた 200 次元の単語埋め込みに対し、Poincaré Embeddings は同等の性能を 5次元 で達成しています。
埋め込みの次元数が小さくとも性能が高いということは、性能を保ったまま計算コストを小さくでき、埋め込みの類似度を計算する必要があるさまざまなタスクにおいて、Poincaré Embeddings を用いることで計算の効率化が期待できます。このことから、理論面の面白さだけでなく実用面の有用性においても、非常に価値の高い手法であると言えるでしょう。
先ほど説明したように双曲空間にはいくつかのモデルが存在しますが、その中でも Poincaré Embeddings はポワンカレ球 (Poincaré Ball) に基づいてデータを表現します。後述しますが、ポワンカレ球ではなくその他の双曲空間のモデルを用いて双曲埋め込みを構成する手法も存在します。このように、採用するモデルによって異なる性質が現れるのも双曲埋め込みの面白い点です。
では、Poincaré Embeddings による埋め込み表現はどのように構築されるのでしょうか。双曲空間にデータを埋め込むというとイメージが難しい印象を受けますが、その実態は比較的シンプルなものです。
Mikolov らが提案した Word2Vec は、文中で共起する単語埋め込み同士の類似度を大きく、それ以外の単語埋め込み同士の類似度を小さくすることで学習を行いました。それに伴い、Mikolov らは CBOW と Skip-gram with negative sampling (SGNS) という二つの単語埋め込みの訓練手法を提案しました。Word2Vec における CBOW と Skip-gram のイメージが以下の図 (Mikolov et al., 2013) です。
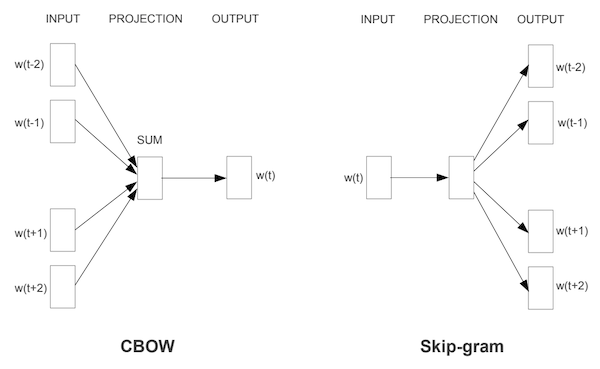
Poincaré Embeddings は、その中でも SGNS に基づき、文中で共起する単語埋め込み同士の、双曲空間における類似度を大きく、それ以外の類似度を小さくするという学習を行います。より具体的には、Poincaré Embeddings は、Word2Vec に以下の変更を加えたものであると言えます。
- 単語埋め込み同士の類似度を「内積」から「双曲空間における距離 $\times (-1)$」に
- 埋め込み表現の最適化を一般的な「SGD」から双曲空間での最適化に対応した「Riemannian SGD」に
それでは、順に二つの要素についてみていきましょう。
双曲空間における埋め込みの類似度
通常の Word2Vec は二つの単語埋め込み (ベクトル) の「内積」を測ることで、二つの単語埋め込みの類似度を計算していました。これに対し Poincaré Embeddings では、双曲空間における類似度を用いることで、双曲空間上での埋め込み表現同士の類似度を計算します。
具体的には、双曲空間における距離に-1をかけたものを用います。なぜ Word2Vec と同様に内積を用いないかというと、双曲空間がベクトル空間ではないため、ユークリッド空間のように内積を自然に定義することができないからです (参考: https://math.stackexchange.com/questions/4015171/inner-product-in-hyperbolic-space)。
ちなみに、双曲埋め込みであっても、埋め込み表現の形式や見た目は通常の埋め込み表現と変わりません (すなわち、ただのベクトルです)。ただ、その埋め込み表現が従う数理的な性質が、ユークリッド空間における埋め込み表現と双曲空間における埋め込み表現で異なるのみです。したがって、上式の $||u-v||$ や $||u||$ は私たちが普段扱っている距離やノルムと同一であり、特別な工夫なく計算することができます。
双曲空間における距離は、空間上の測地線 (geodesics) の長さで表すことができます。双曲空間における距離をより直感的に理解するため、以下の双曲空間上の点同士の距離(測地線)を表現した図を見てみましょう。図は Cetin et al., 2022 からの引用です。
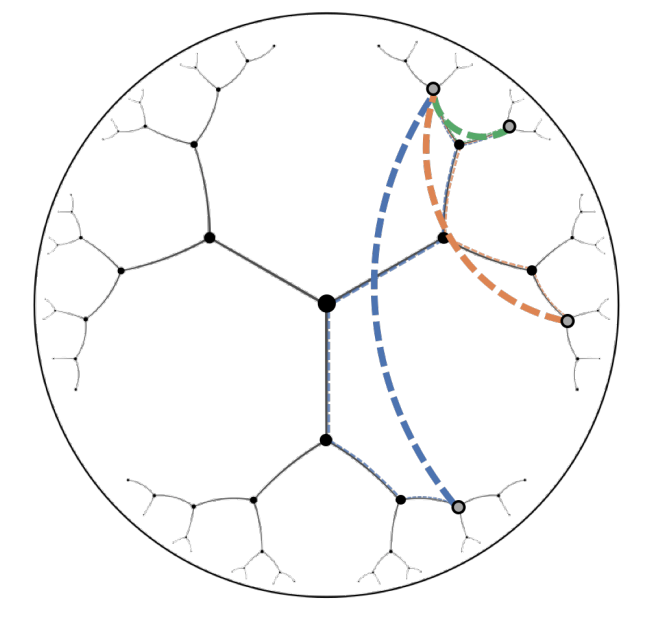
この図では、最も上にある灰色の点を視点とした時に、その他の点との測地線が、双曲空間においてどのように表せるかを緑・橙・青の3色で図示しています。ユークリッド空間では点と点との距離は、2点間を結ぶ線分の長さで表現することができました。それに対し、双曲空間では円弧の長さが距離を表現していることがわかると思います。
実際には、双曲空間上での距離は以下で定義されます。
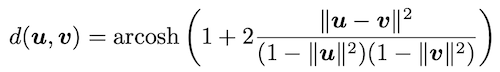
ここで、式中の $||\cdot||$ は通常のユークリッドノルムを表します。距離に双曲線余弦関数の逆関数 (arcosh) が出てきているのが少しびっくりしますが、その他はベクトルのノルムを計算するなどのそれほど複雑ではない計算が主です。
さらに理解を深めるため、上記の距離を計算するための、Python と PyTorch を用いた擬似コードを以下に示します。疑似コードはhttps://github.com/facebookresearch/poincare-embeddings/blob/main/hype/manifolds/poincare.py を参考に https://carbon.now.sh/ で画像を生成したものです。

擬似コードからも、双曲埋め込みといえど、そこまで複雑な計算をしていないということがわかっていただけるのではないでしょうか。Poincaré Embeddings では、この双曲空間における距離に -1 をかけ、いくつかのハイパーパラメータを加えたものを類似度として用います。
双曲空間における最適化
一般的に、深層学習では損失関数を定義したのち、勾配降下法を用いてモデルパラメータをどのように更新すれば良いかを計算し、パラメータを更新します。この最適化の方針は双曲埋め込みの場合でも、さらに言えば一般の多様体上での最適化でも同じように適用できますが、ユークリッド空間上での最適化に一工夫加える必要があります。
どのような工夫を加える必要があるのか、例を使って考えてみましょう。先ほどと同様、多様体の例として地球平面を用いて、地球平面上の点Aと点Bについて考えてみます。そして、点Aから点Bまでを最短距離で移動したいとします。
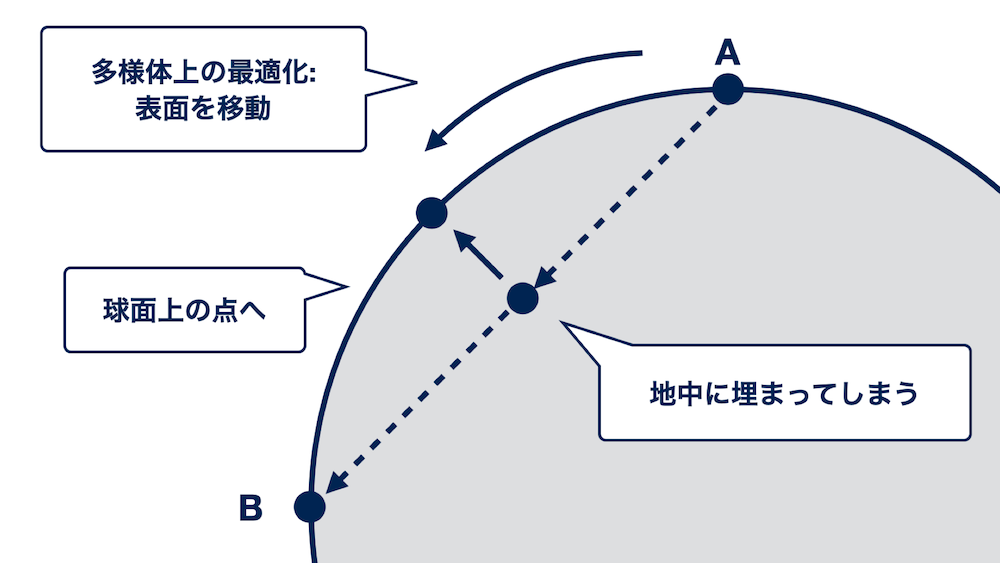
この場合、3次元空間上で生きる私たちにとっては、地球に穴を開けながら真っ直ぐ進むのが最短経路になります。しかし、地球平面上での移動に限定する場合、このように"直線的な"移動はできず、地球表面の上しか動くことができなくなります。その場合、地球平面を沿うように弧を描き、直線的な最短経路の"上"をすべるように移動するのが最短経路になるでしょう。
これと同様の事象が、一般のリーマン多様体上での最適化でも発生します。機械学習のパラメータ最適化とのアナロジーを考えると、先ほどの例の点Aは更新前のモデルパラメータであり、点Bは更新後に最終的に辿り着くモデルパラメータになります。つまり、先ほどの例における点Aから点Bへの矢印は、点Aから点Bへの最短距離を移動するための進むべき方向、すなわち勾配を表していると考えることができます。
さて、私たちはいま双曲空間上にデータを埋め込みたいのでした。双曲空間も球面と同様歪んだ空間ですので、同様の問題が生じます。このような問題に対処し、多様体上での最適化を行うのが、双曲埋め込みのもう一つのポイントです。
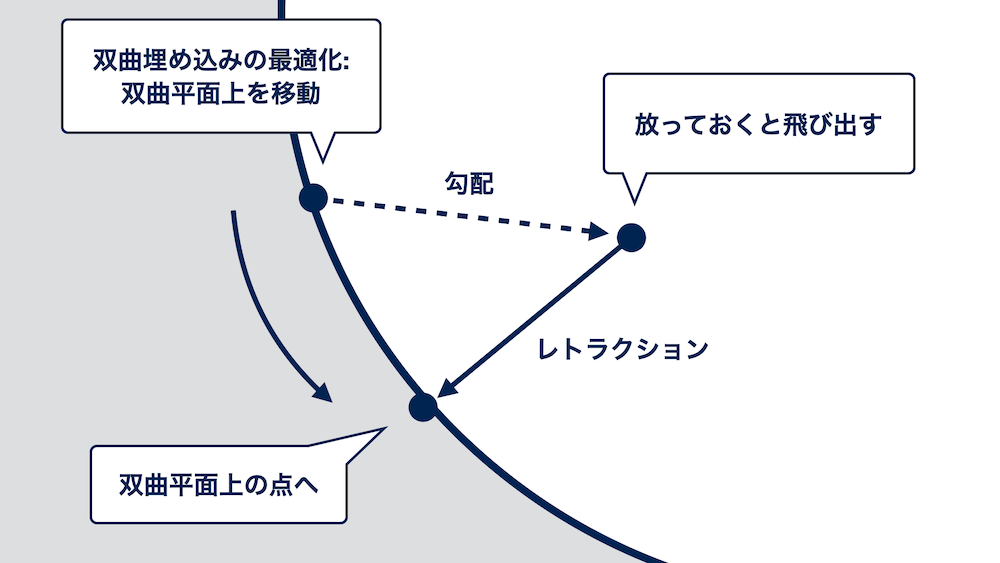
まず、リーマン多様体上での最適化では、ユークリッド空間上での最適化と同様に、損失関数をもとに、ある点におけるユークリッド空間上での勾配を計算します。次に、その勾配に後処理を加えたのち、勾配を加えた後の点がちゃんと多様体上に存在するよう、飛び出た点を多様体上に引き戻すレトラクションという操作を行います。これにより、多様体上にいながら損失を小さくする方向に近づくことができたので、繰り返しこの手順を重ねることでさらに損失を小さくしていきます。
上記の手順で、双曲埋め込みを学習することでできます。より詳細な内容については、Riemannian SGD を提案した論文 (Bonnabel, 2013) をご参照ください。また、Poincaré Embeddingsを理解する上で重要な要素である「双曲空間上の距離」と「Riemannian SGD」については、GitHub 上で公開されている実装も非常に参考になりますので、あわせてご覧ください。
評価実験
Nickel らは複数の実験で、既存の単語埋め込みと比較した際の、Poincaré Embeddings の有用性を評価しました。特に、WordNet に存在する階層構造をうまく再現できるか、訓練データに含まれない階層関係を当てられるかというタスクについて、既存の単語埋め込みと Poincaré Embeddings を、5, 10, 20, 50, 100, 200 次元の6通りで構築し、実験した結果が以下の表です。
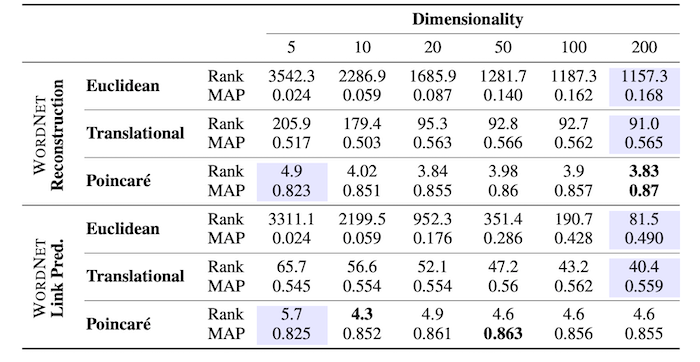
Rank は平均順位 (Mean Rank) を表し、小さい方が良い指標です。MAP は平均適合率の平均 (Mean Average Precision) を表し、大きい方が良い指標です。
表より、Poincaré Embeddings が一貫して非常に高い性能を示しています。また、既存の手法に対して、Poincaré Embeddings が同等かそれ以上の性能を発揮した最小の次元数に対応する部分が水色で強調されていますが、既存の Word2Vec による 200 次元の単語埋め込みよりもはるかに高い性能を、Poincaré Embeddings が5次元で達成していることがわかります。以上から、既存の単語埋め込みと比較して、Poincaré Embeddings は階層構造を適切に表現することができていると言えます。
現在、Poincaré Embeddings は NLP における有名な手法やアルゴリズムが集まったソフトウェアである Gensim から簡単に利用することができます。
https://radimrehurek.com/gensim/models/poincare.html
みなさんもお手元の階層関係があるデータを用いて、Poincaré Embeddings を訓練してみてはいかがでしょうか。
Lorentz Embeddings
こちらの研究も、Poincaré Embeddings 論文の著者である Nickel 氏によるものです。
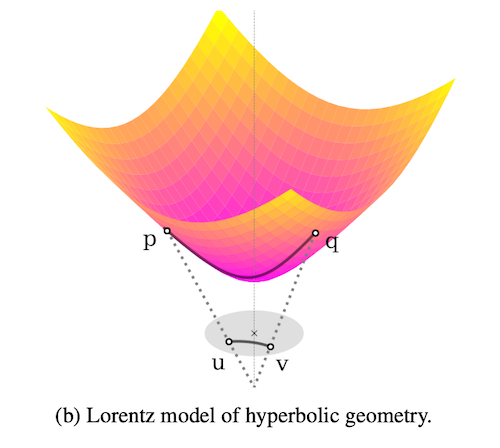
先述の通り、双曲空間のモデルにはいくつかの種類があります。本研究では、その中でもローレンツモデル (Lorentz model, 別名 hyperboloid model)を用いることで、ポワンカレ球モデルを用いるよりも安定して効率的に埋め込み表現を構成できることを示したというものです。Lorentz Embeddings では、ローレンツモデルにおける距離を以下のように定義します。
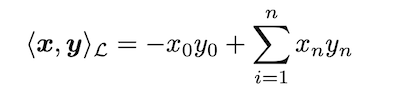
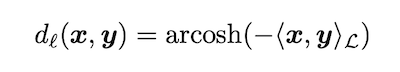
上記の定義により、Poincaré Embeddings とは異なり、距離の計算に分数が含まれなくなります。Poincaré Embeddings における距離の計算には分数が混ざっており、特に埋め込みのノルムが1に近い場合に距離が極めて大きくなってしまうという数値計算上の不安定性がありました。
Lorentz Embeddings ではこの問題を解決するため、より単純で数値的に安定した、つまり浮動小数点数の計算時のオーバーフローやアンダーフローの危険性が少ない距離関数を用いて、埋め込み表現を獲得します。
実験では、名詞・動詞や医療用語の階層構造を正しく捉えられているかを評価しています。実験の結果を示したのが以下の表です。
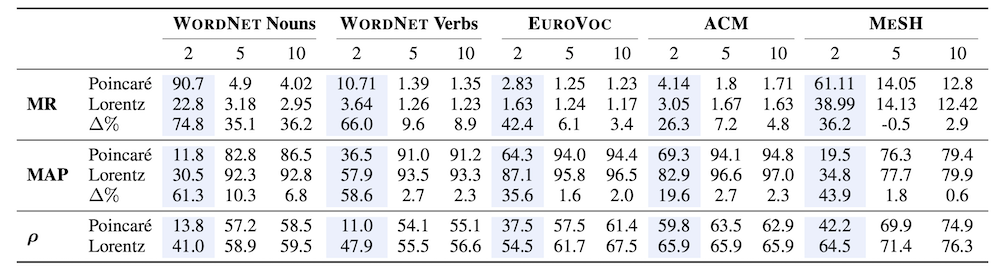
MR は平均順位 (Mean Rank) を表し、小さい方が良い指標です。MAP は平均適合率の平均 (Mean Average Precision) を表し、大きい方が良い指標です。$\rho$ はスピアマンの順位相関係数を表し、大きい方が良い指標であり、△%は Poincaré Embeddings と比較して Lorentz Embeddings の性能がどの程度向上したかを表します。さらに、各列の上に表記されている数字は埋め込みの次元数を表します (今回の実験では2, 5, 10次元の3通り)。
表から、Lorentz Embeddings が Poincaré Embeddings よりも一貫して高い性能を示しており、特に2次元などの極めて小さい次元 (水色で強調されている部分) で埋め込み表現を学習したときに大きく性能が向上していることがわかります。
このように、Poincaré Embeddings では数値計算の不安定性から性能が低下してしまうことがありましたが、Lorentz Embeddings ではローレンツモデルという異なる種類の双曲空間のモデルを用いることで、より安定的・効率的に双曲埋め込みを得られることを示しました。
Hyperbolic Entailment Cones
元論文: Ganea et al., ICML 2018. Hyperbolic Entailment Cones for Learning Hierarchical Embeddings
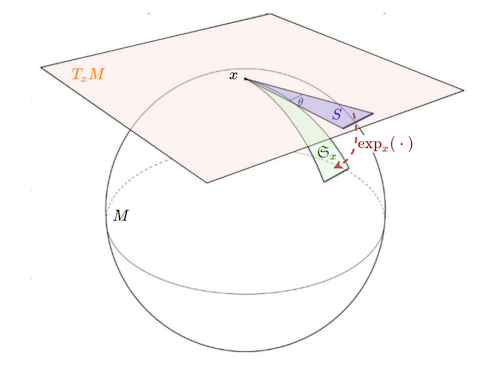
Genea らによって提案された Hyperbolic Entailment Cones は、双曲空間で領域的な表現を構成する手法です。上図の緑色で塗られた区画が示すように、Hyperbolic Entailment Cones ではある点を頂点とする"錐"を考えます。そして、あるデータを頂点とする錐と、その錐が包含する錐について、それらのデータ同士の包含関係を対応させます。
Poincaré Embeddings では、双曲空間上での距離で階層構造を表現していましたが、Hyperbolic Entailment Cones では錐を考えることで、より明確にデータ同士の順序構造を考えることができます。
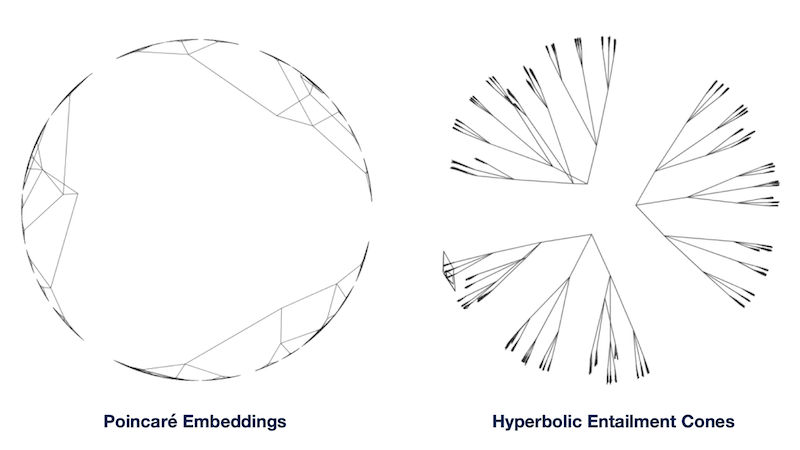
実験の結果、Hyperbolic Entailment Cones を用いることで、Poincaré Embeddings ではうまく階層構造を捉えきれないような場合でも適切に階層構造を捉えた埋め込み表現を獲得できることがわかりました。
Hyperbolic Disk Embeddings
元論文: Suzuki et al., ICML 2019. Hyperbolic Disk Embeddings for Directed Acyclic Graphs
Suzuki らが提案した Hyperbolic Disk Embeddings は、双曲空間上に Disk Embedding という領域的な埋め込み表現を構築する手法です。
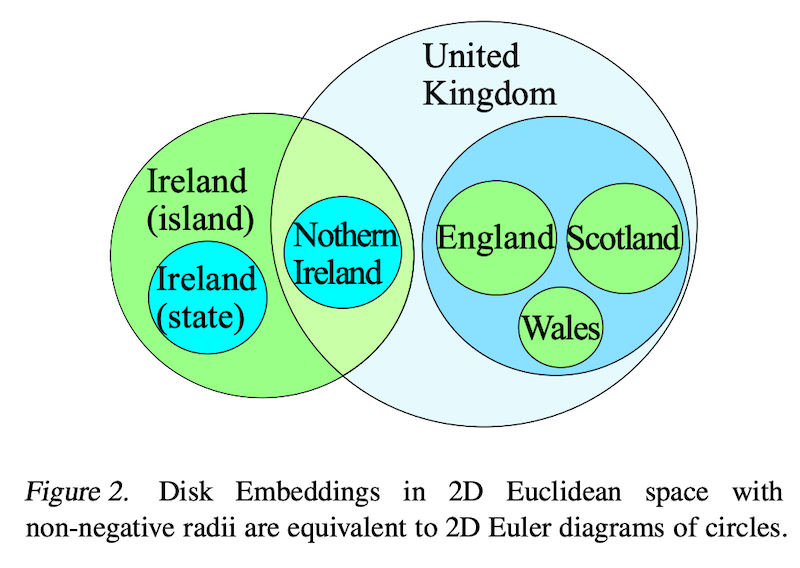
Suzuki らは Hyperbolic Entailment Cones の考えをさらに発展させ、既存の双曲的・領域的な手法を統一的に解釈できるフレームワークを提案しました。
実験の結果、提案手法である Hyperbolic Disk Embeddings は、既存の Poincaré Embeddings や Hyperbolic Entailment Conesと比較して、木構造や有向非巡回グラフ (Directed Acyclic Graph: DAG) といった複雑な階層構造をより適切に表現できたとのことです。
双曲埋め込みの応用
これまでに、データを双曲空間上で表現する手法について紹介してきました。双曲空間の特性を用いることで、データの階層関係を適切に捉えた表現を得られるのは、双曲埋め込みの大きな利点です。この節では、双曲埋め込みの利点を活用した研究について見てみましょう。
Poincaré GloVe
元論文: Tifrea et al., 2018. Poincaré GloVe: Hyperbolic Word Embeddings
Nickel らが提案した Poincaré Embeddings は、階層構造がラベル付けされた教師データを用い、教師あり学習で単語の階層関係を捉えた単語埋め込みを獲得する手法でした。Tifrea らが提案した Poincaré GloVe は、教師なし学習によって品質の高い単語埋め込みを獲得する GloVe と同様に、Poincaré Embeddings を用いて教師なしで単語の階層関係を捉えた単語埋め込みを獲得する手法です。
実験では、通常のユークリッド空間での単語埋め込みである GloVe では難しかった、単語の意味と階層構造の双方を適切に捉えた埋め込み表現を構成できていたとのことです。
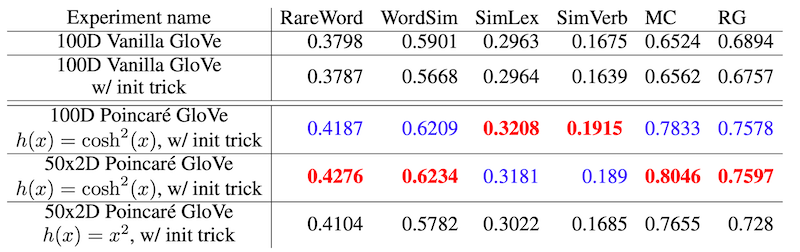
本研究はこのほかにも、双曲埋め込みと、データをガウス分布で表現する手法であるガウス埋め込みとの関係についての議論もされており、よりよい埋め込み表現とは何かを考える上で参考になりそうです。
このほかにも、テキストを双曲空間に埋め込む手法には以下のようなものがあります。
- Dhingra et al., TextGraphs 2018. Embedding Text in Hyperbolic Spaces
- Gu et al., ICLR 2019. Learning Mixed-Curvature Representations in Product Spaces. OpenReview
双曲的なニューラルネットワーク
元論文: Shimizu et al., ICLR 2021. Hyperbolic Neural Networks++
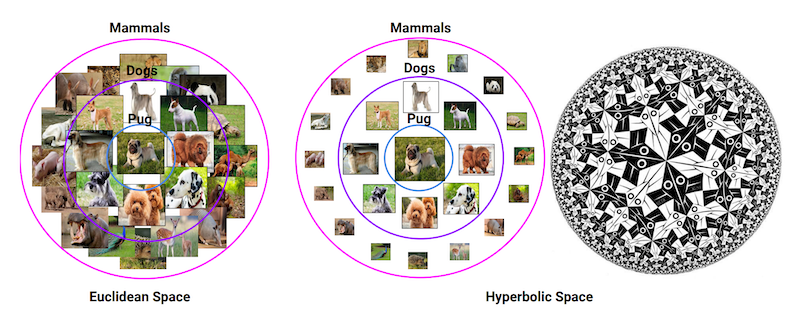
これまでに紹介した研究は、双曲埋め込みを直接用いて単語の階層関係や類似度を測っていました。しかし、通常の埋め込み表現の用途はそれだけではありません。例えば、自然言語処理では文を単語埋め込みの系列に変換し、全結合層・畳み込み層・注意機構といった層に通すといった手順によって、単語埋め込みを文の分類など多様なタスクに適用することができます。
双曲埋め込みでも同様の手順を実施することは可能でしょうか。つまり、双曲埋め込みを入力とする深層学習モデルを考えることは可能でしょうか。前提として、通常のニューラルネットワークで双曲埋め込みの利点を活用することは困難です。なぜなら、通常のニューラルネットワークは入力されるベクトルがユークリッド空間上に存在することを想定しており、何も工夫をしないと、入力された双曲埋め込みは、ユークリッド空間上のベクトルとして演算されてしまうからです。すなわち、出力されるベクトルが、入力されるベクトルと同じ双曲空間上に存在するとは限りません。
せっかく低次元でも適切に階層構造を捉えられる埋め込み表現を得られたので、これをうまく活用したニューラルネットワークを構成したいところです。この問題に対し、双曲空間上のニューラルネットワークを構成する手法がいくつか提案されてきました。
- Ganea et al., 2018. Hyperbolic Neural Networks
- Gulcehre et al., 2018. Hyperbolic Attention Networks
- Liu et al., NeurIPS 2019. Hyperbolic Graph Neural Networks
しかし、既存の手法はユークリッド空間上のニューラルネットワークと異なり、追加の計算コストが必要になる、できる演算が限られているなどの問題がありました。これらの問題に対し統一的な解決策を提案したのが、Shimizu らの Hyperbolic Neural Networks++ です。
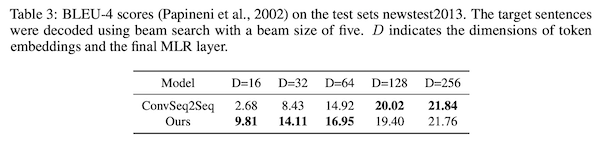
実験の結果、機械翻訳などのさまざまなタスクで有効性を確認し、特に埋め込み表現が低次元の時に高い性能を達成しました。
Hyperbolic Deep Reinforcement Learning
元論文: Cetin et al. 2022. Hyperbolic Deep Reinforcement Learning
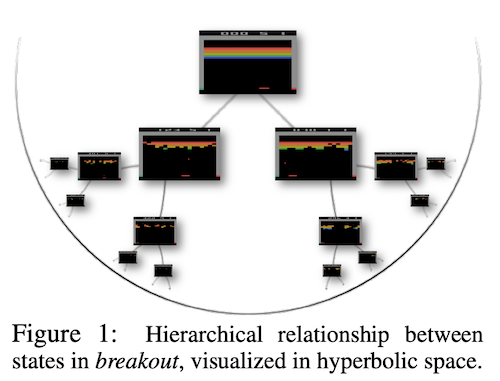
最後に、深層強化学習に双曲埋め込みを用いることで強化学習における"状態"の階層関係を捉えた学習を行う手法である、Hyperbolic Deep Reinforcement Learning について紹介します。
実世界の物質を操作することを目的とした機械学習、具体的にはゲームやロボットの操作を行う機械学習モデルを構築する上で、強化学習は重要な要素技術です。しかし、既存の強化学習手法は、極めて大規模な訓練データや個々のタスク特有のテクニックなどに依存しており、極めて多岐にわたる実世界のタスク設定に汎用的に適用することは難しいです。
著者らはこの強化学習における問題を「制御のための汎化可能な特徴を効率的に学習するための適切な事前分布の不足」によるものだと主張し、これを解決するために、双曲空間の特性を活かした強化学習手法を提案しました。具体的には、強化学習における「状態」と「行動」が成す木の階層構造を、双曲埋め込みを用いることで自然にモデリングします。
さらに、著者らは深層強化学習において双曲埋め込みをエンドツーエンドで安定的に学習する手法であるスペクトル正則化双曲写像 (spectrally-regularized hyperbolic mappings: S-RYM) を提案しました。
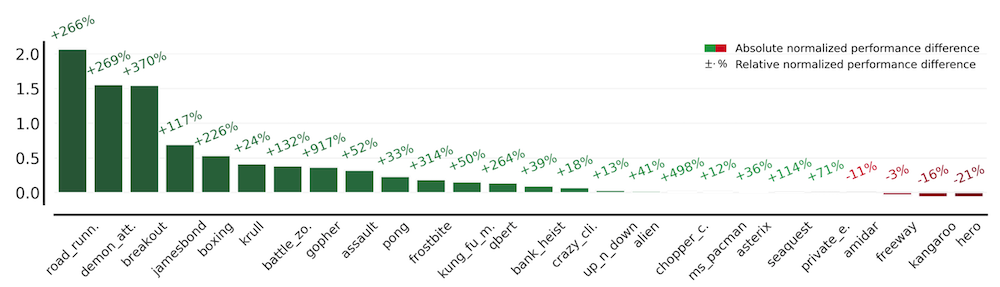
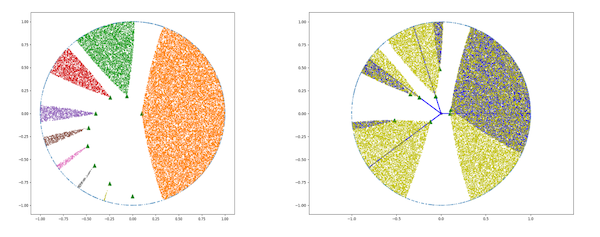
さらに、得られた双曲埋め込みを2次元のポワンカレ円板状に可視化したのが以下の図です。
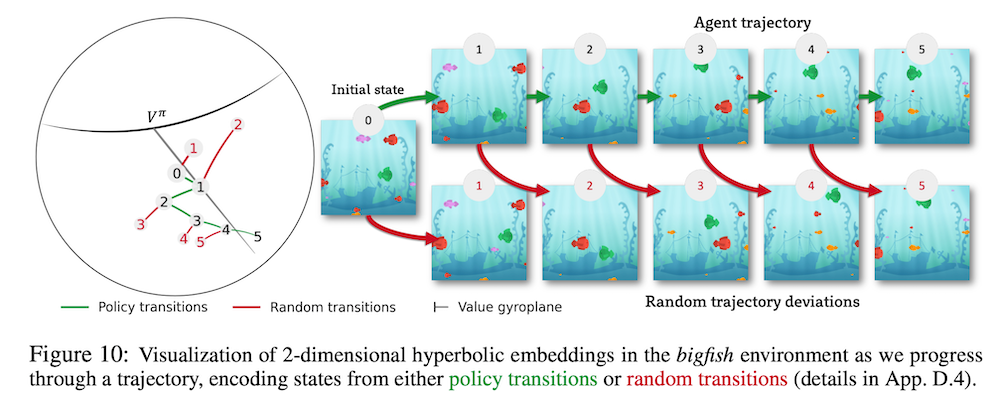
この図は、Procgen (Cobbe et al., 2019) という強化学習におけるベンチマークの、bigfish というゲームにおける各状態 (図の右側) において、それらの状態に対応した双曲埋め込みを図示したもの (図の左側) です。bigfish は、自身が緑色の魚を操作し、自分より小さな魚を食べることで成長でき、かつ小さな報酬が得られます。
また、最終的にすべての魚より大きくなったらクリアとなり、その際は強化学習のエージェントに対して大きな報酬が与えられるというゲームです。このbigfish というタスクでは、画面中に新たな魚が現れるほど、魚を食べることによる報酬が得られます。
可視化結果から、実際に画面中に新たな魚や障害物が現れたタイミングで、双曲埋め込みの大きさが大きくなっており、これが強化学習における各状態の複雑さ(操作の繊細さ) や将来の報酬の期待値と不確実性に関連しているという傾向が観察できたとのことです。
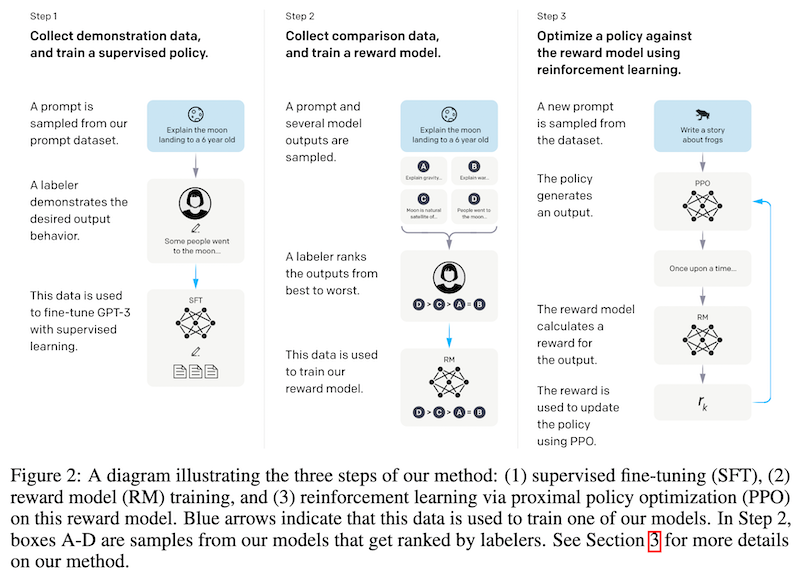
本研究で用いられている強化学習アルゴリズムの PPO は、非常に自然な対話が可能なことで先日有名になった ChatGPT でも用いられていると考えられている技術です。ChatGPT の技術解説については、以下の記事で紹介していますのでぜひご覧ください。
おわりに
本記事では、データを双曲空間上で表現する双曲埋め込みについて紹介しました。双曲埋め込みは理論的に強固なバックグラウンドを持ち、歪んだ空間の特性を活かして階層構造をうまく捉えられるという非常に面白い手法です。また、双曲埋め込みは、それ自体非常に興味深い研究対象であるとともに、有望な応用も続々と発表されていることから、今後も注目すべき分野の一つにであると言えるでしょう。
一方で、双曲埋め込みの有効性が最も発揮されるのは、埋め込み次元が低次元の場合であることが多く、この点については、通常のユークリッド空間での埋め込み表現との関連や、次元数を大きくした場合の双曲埋め込みの振る舞いの変化など、気になる事項も多く存在しています。今後も、双曲埋め込みをはじめとする、「歪んだ空間」の埋め込み表現に注目です。
文責:塚越 駿(名古屋大学)
参考文献:
- Poincaré Embeddings による職種の類似度計算とその利用
- Riemann多様体上の連続最適化
- 異空間への埋め込み!Poincare Embeddingsが拓く表現学習の新展開
- 双曲空間でのMachine Learningの最近の進展
- https://www1.econ.hit-u.ac.jp/kawahira/courses/kiso/04-mfd.pdf
- http://www.math.titech.ac.jp/~kotaro/class/2017/geom-a/lecture-06.pdf
関連記事