近年、単語をベクトルとして表現するベクトル表現が広く一般に用いられるようになりました。一方で、ベクトルでは表現できないデータも多く存在しており、その代表例が意味や概念の階層関係です。多義語に代表されるように、自然言語における単語は複数の意味を持ち、単語ごとに異なる意味の広がりを持つと考えるのが自然ですが、現在の単語ベクトル表現ではこのような単語の性質をうまく表現することができていません。
本記事で紹介する Box Embedding はこのような問題を解決するために、データを「点」ではなく「箱」で表現することで、交差や包含関係といったデータ同士のより豊かな関係性を捉えます。特に本記事では、教師なし学習によって単語の「箱」を獲得する Word2Box と呼ばれる手法を中心に、前提知識から丁寧に解説します。
文責:塚越 駿(名古屋大学)
ステート・オブ・AI ガイドでは、人工知能・機械学習分野の最新動向についての高品質な記事を毎月5〜6本配信しています。購読などの詳細につきましては、こちらをご覧ください。また、Twitter アカウントの方でも情報を発信しています。
ベクトル表現と領域表現
本記事で取り上げるBox Embedding について紹介する前に、近年の機械学習における基礎技術の一つであるベクトル表現と、ベクトル表現の問題点を解決するために生まれた領域表現 (region-based representation) について紹介します。
ベクトル表現は、自然言語処理や画像処理をはじめとする深層学習分野全般で用いられている、非常に基礎的な技術です。特に、Word2Vec や BERT に代表される単語埋め込み (word embedding) は、自然言語処理において欠かせない技術となっています。
単語埋め込みは、単語を実数ベクトル、つまり数値の列で表現します。このベクトルに対して、「意味的に近い単語のベクトル同士が実数空間上でも近くに存在するように」という要請をモデルの目的関数に組み込むことで、訓練の結果得られる単語埋め込みは、その単語の意味を反映したものになります。
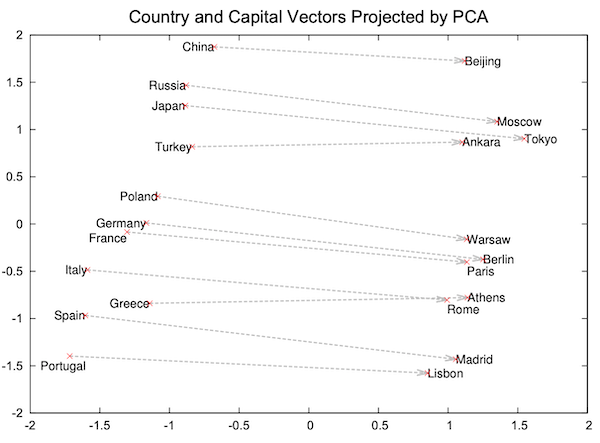
上図は国と都市の名前に対応した単語埋め込みを2次元空間上で可視化したものです (Mikolov et al., 2013 より引用)。国と都市がそれぞれ集まっており、似た概念の単語が近くに分布していることが確認できます。
単語埋め込みの非常に興味深い性質として、このような目的関数を用いて単語をベクトルとして表現・訓練することで、ベクトルの演算によって単語の意味の演算を行えることが示されています。
例えば、「王」-「男」+「女」=「女王」のように、それぞれの単語のベクトル表現の演算によって、自然な意味の演算が実現できるのです。
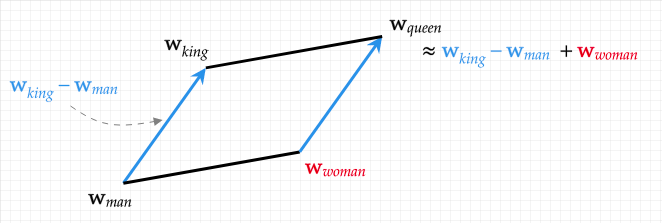
上図は「king」「queen」「man」「woman」に対応する単語埋め込みの幾何学的関係を示したもので、ベクトル演算で表現される幾何学的関係と単語の意味の関係が対応していることが確認できます (引用元)。
さて、機械学習分野ではもはや当たり前に用いられ、その性質は熱心に研究されていますが、ベクトル表現では解決できない問題も知られています。
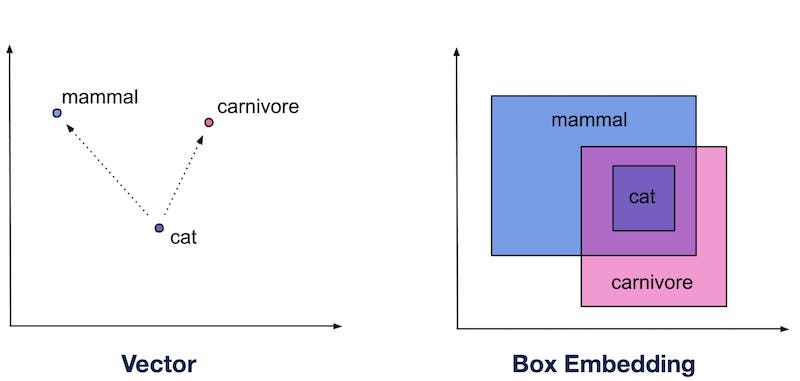
その中でも代表的な問題が「データを点でしか表現できない」というものです。具体的には、ベクトル表現はただの「点」でしかないので、意味の包含関係や概念の階層関係といった集合的な性質が必要になる関係性を自然に表現することができません。
例えば、「動物」と「犬」という二つの単語について考えてみると、「動物」は「犬」や「猫」という概念を包含するので、意味空間で「動物」は「犬」よりも意味的に大きな広がりを持ちそうです。しかし、ベクトル表現では「動物」も「犬」も点でしか表現できないため、このような意味の広がりの違いを表現することができません。
これらの問題を解決するために提案されたのが領域表現 (region-based representation) です。領域表現を用いることで、ただの点による表現を超えて、より複雑なデータの関係性を表現することができるようになります。
領域表現の「領域」には、さまざまな選択肢が考えられます。自然言語処理における領域表現の草分け的な手法である Gaussian Embedding (Vilnis et al. ICLR 2015) は、単語をガウス分布 (Gaussian distribution) で表現しました。
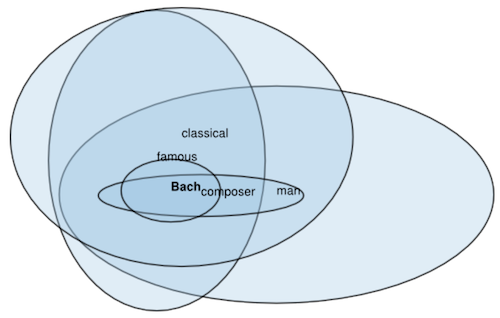
上図はガウス分布で表現された単語の階層関係を可視化したもので、Vilnis et al., 2015 からの引用です。より意味的に狭い単語は、より分散の小さいガウス分布で表現されます。
また、Poincaré Embedding (Nickel et al. NIPS 2017) は、双曲幾何学に基づき、単語や事物を双曲空間上で表現することで、階層関係や意味の重なりを捉えた表現を獲得しました。
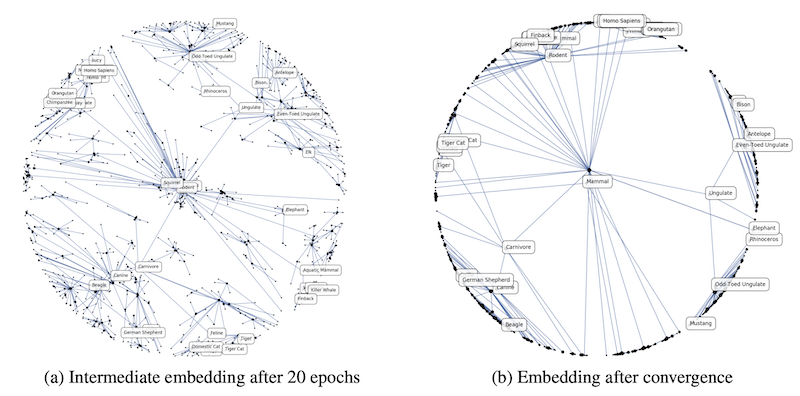
上図は双曲空間上で表現された単語の階層関係を可視化したもので、Nickel et al., 2017 からの引用です。
このように、より良い領域表現を求めて、現在でも様々な表現形式が模索されています。
本記事では、領域表現の中でも、データを「箱」で表現する Box Embedding について紹介します。Box Embedding は近年最も応用が広がりつつある領域表現手法の一つであり、Gaussian Embedding や Poincaré Embedding と比較して、「箱」で表現される領域同士の重なりが計算しやすいという利点があります。
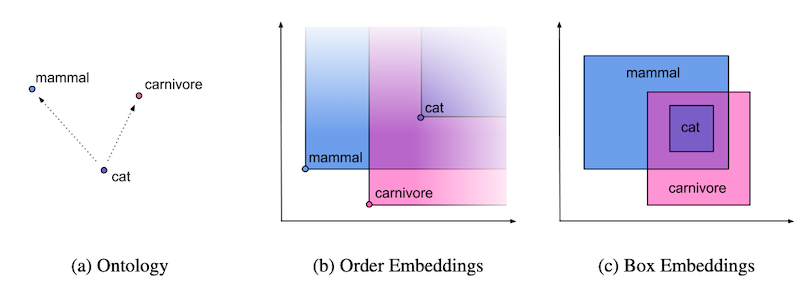
以下の図は Chheda et al., 2021 より引用したもので、自然言語における階層関係 (a) と、Box Embedding を用いてデータを「箱」として表現した際の包含関係 (b) を可視化したものです。
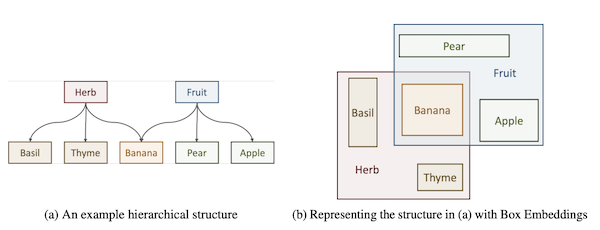
Box Embedding を扱う研究はいくつか存在しますが、その中でも本記事では、教師なし学習によって単語の Box Embedding を獲得する Word2Box と呼ばれる手法を中心に紹介します。
Word2Box は、Box Embedding に関するいくつかの研究成果に基づいて提案された手法です。したがって、本記事ではまず Word2Box が基づく重要な技術について順に紹介します。
具体的には、初めて単語を「箱」で表現した手法である Box Lattice、Box Lattice の最適化上の問題を解決するために提案された手法である Smoothed Box、Smoothed Box をさらに改善した Gumbel Box の順に紹介し、最後に Word2Box について紹介します。
Box Lattice
元論文: Vilnis et al., 2018. Probabilistic Embedding of Knowledge Graphs with Box Lattice Measures
データを「箱」で表現する Box Embedding のアイデアは、この論文で提案されました。
まずは、データを「箱」で表現するイメージを具体的に掴むため、いくつかの語に対して、Box Lattice を用いて得られた「箱」を可視化した以下の図を見てみましょう。
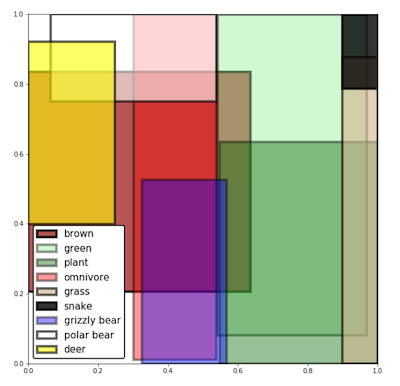
図から、「plant」と「green」が大きく重なっている、「brown」と「grizzly bear」が一部重なっているなどの結果を観察することができます。
このように、ベクトル表現ではデータをただの「点」でしか表現できませんでしたが、データの表現形式として「箱」を用いることで単語同士の意味的・概念的階層関係を自然に表現することができるようになります。
Vilnis らが提案した Box Embedding では、d次元空間における「箱」を $d$ 個の「始点」と「終点」のペアで表現します。つまり、通常のベクトル表現と比較して、2倍の次元数の数値を用いてあるデータを表現することになります。
以下に、2次元の Box Embedding の実装上のイメージを表した図を示します。A と B の箱それぞれに対して、z と Z の二つのパラメータが存在し、z と Z によって「箱」が定義されます。 図は Chheda et al., 2021 からの引用です。
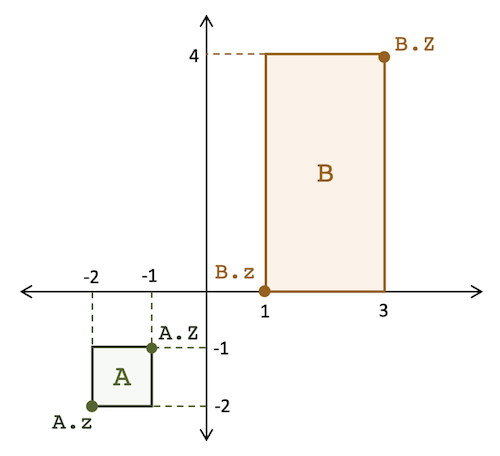
Vilnis らが提案した Box Lattice を用いれば、意味の広がりやデータ同士の重なり具合を非常に簡単に計算することができます。具体的には、意味の広がりは「箱」の体積で表現でき、重なりは各次元において min と max を適切に取ることで評価できます。
「箱」を用いればデータの広がりや重なりは非常に簡単に求めることができます。一方で、このような「箱」はどのように学習すればよいのでしょうか。
大まかな方針としては、「箱」同士の階層関係が示された教師データを用い、$d$ 次元空間において階層関係の上位にあたる「箱」が下位にあたる「箱」を含むようにすればよさそうです。つまり、上位下位関係にある箱同士の重なりが大きくなるように学習を行えばよさそうです。
この方針を検証するため、Vilnis らは英語の単語・概念辞書として有名な WordNet を用いた実験を中心に、Box Lattice の有効性を示しました。
実験の結果、ガウス分布や半空間を用いる既存の領域表現手法と比較して良好な性能を達成しました。
階層関係を表現する教師データがあれば、Box Lattice は自然言語に限らず多様な階層関係を表現することができます。本論文の対象である自然言語以外にも、包含関係・部分的な階層関係は実世界で随所に確認でき、Box Embedding のさまざまなデータへの応用が考えられそうです。その意味で、Box Lattice は非常に応用範囲の広い技術であるといえるでしょう。
Smoothed Box
元論文: Li et al., ICLR 2019. Smoothing The Geometry of Probabilistic Box Embeddings
Vilnis らによって提案された Box Lattice は、データを「箱」で表現するという革新的な技術でしたが、厄介なことに最適化が難しいという問題がありました。
具体的には、Box Lattice の訓練において、「箱」同士が重なるときはその勾配を計算することができるものの、「箱」同士が重ならないときは重なり部分の体積が 0 となってしまいます。
これでは、「箱」同士が重なっていない場合の勾配が 0 になってしまう、つまりそれぞれの「箱」同士がどれくらい近づく/離れるべきかがわからないので最適化が難しい、という問題が生じます。特に、高次元空間ではほとんどの「箱」のペアは重なりを持たないと考えられ、学習中に「箱」同士をどの程度近づければよいかわからない状況が多くなるため、この問題はより深刻になります。
Vilnis らは「箱」の重なりに関してその下限値を最大化するという方針でこの問題を回避していますが、これでは目的の表現を直接最適化しているとは言えません。
本論文で Li らによって提案された Smoothed Box は、「箱」を滑らかにすることでこの問題をより直接的に解決し、最終的に得られる表現の品質を向上させるというものです。
Li らの手法のアイデアは、訓練時に「箱」同士の重なりを考慮する際、「箱」の端をぼかす処理を加えるというものです。これにより、「箱」の重なりの体積が 0 になってしまうのを防ぎ、「箱」同士の位置関係をよりうまく最適化することができます。
より詳細には、以下の図に示すようなガウスカーネルを用いた畳み込み処理を参考に、「箱」をぼかすための関数を設計して利用するというものです。
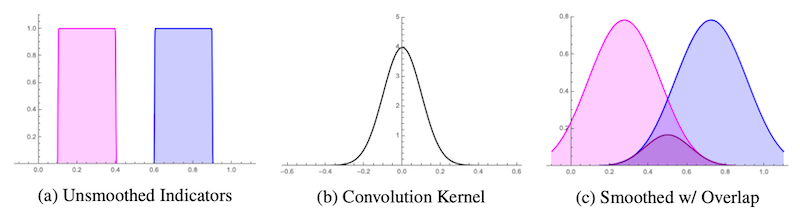
Smoothed Box の有効性を示すため、Li らは WordNet を用いた実験を中心に評価を行なっています。
実験の結果、Smoothed Box は Box Lattice と比較して、データが潤沢に存在する場合は Box Lattice と同等程度の性能であるものの、データの分布が不均衡であるときに既存手法よりも遥かに高い性能を示すことがわかりました。
これは、「箱」をぼかすことによってデータが不均衡であるような場合でもうまく最適化ができるようになったためだと考察されています。
Gumbel Box
元論文: Dasgupta et al., NeurIPS 2020. Improving Local Identifiability in Probabilistic Box Embeddings
Dasgupta らによって提案された Gumbel Boxは、Smoothed Box を提案した Li らと同様、「箱」の端をぼかすことで Box Embedding の最適化をうまくできるようにするというものです。
Smoothed Box では「箱」をぼかすための手段としてガウス分布を用いました。一見、この選択は自然なものに見えますが、このガウス分布によるぼかしは、果たして Box Embedding のための最適な手段と言えるのでしょうか。
Dasgupta らはこの点について、既存手法が解決できていない「箱」の最適化上の事例に基づき、Smoothed Box では「箱」の重なり方や位置関係の違いを区別できない場合があるという「局所的識別性の問題」(local identifiability problem) を指摘し、「箱」をぼかすための手段として Gumbel 分布を用いることでこの問題を解決する手法を提案しました。
局所的識別性の問題について具体例を用いて述べます。まずは、Smoothed Box をはじめとする既存手法で考慮できていない「箱」同士の関係性について考えてみましょう。
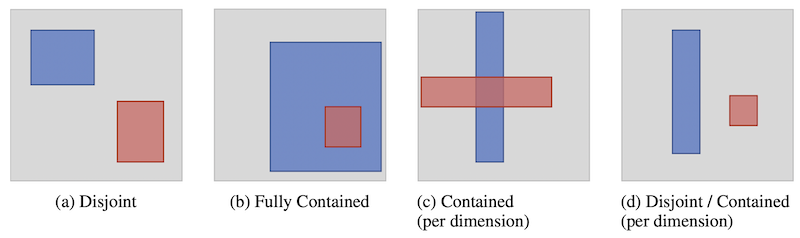
上の画像では、Box Embedding の最適化について考える際の、ありうる二つの「箱」の位置関係のうち、ぼかしていない「箱」では最適化上の問題が生じるものを示しています。
例えば、(a) の例は、青色で示される箱と赤色で示される箱が交差しておらず、勾配を計算することができません。この事例については、Smoothed Box で最適化をすることができるようになっていますが、では (b) や (c) の事例ではどうでしょうか。
(b) では赤色の箱が青色の箱に完全に含まれており、Smoothed Box を用いる場合には青色の箱内での赤色の箱の位置がどの位置になるべきかがわかりません。また、(c) で示されるように、青色の箱や赤色の箱を多少動かしても、交差部分の体積が全く変化しない状況も存在します。さらに、(d) のように青色の箱に対して赤色の箱を縦にある程度並行移動しても、位置関係が変化しない場合もあります。
このように、既存手法である Smoothed Box では「箱」同士がどのように位置・交差すべきかという点を考慮しきれていませんでした。Gumbel Box の最も重要なアイデアは、Gumbel 分布を Box Embedding の最適化に用いることです。
まず、Gumbel 分布について説明します。 Gumbel 分布とは、ある確率分布に従う確率変数の最大値が従う連続確率分布の一種です。Gumbel 分布を用いると、例えば年ごとに増減する人口を確率変数とみなした場合に、次の年の人口の最大値がどれくらいになるかを確率分布を用いて推定することが可能になります。
さきほど、「箱」の重なりを計算する際の「箱」の両端は、各次元の min と max を適切に取ることで決定できると説明しました。この事実に注目すると、「箱」の両端が確率的に分布すると考えたとき、「箱」の重なりの両端は Gumbel 分布に従うと考えられます。
「箱」の端を確率分布でモデル化する Gumbel 分布を用いることで、「箱」同士の位置関係をより適切に最適化できるのではないかというのが Gumbel Box の動機です。
Gumbel Box を用いると、訓練中に「箱」は下図のようにぼかされることになります。図は Boratko et al., 2021 からの引用です。
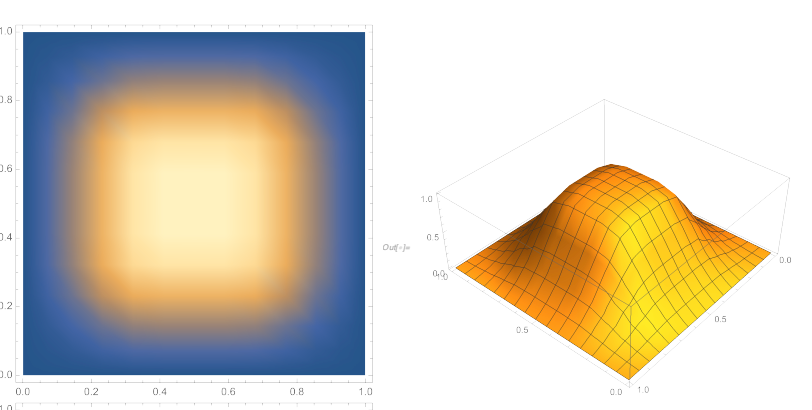
このようなぼかし方により、空間上での二つの「箱」の重なり方 (交差部分の体積の変化の仕方) が Smoothed Box とは変化します。
具体的には、Smoothed Box が以下の図の左側のようなカクカクとした重なり方をするのに対して、Gumbel Box は図の右側のような円形の重なり方をします。
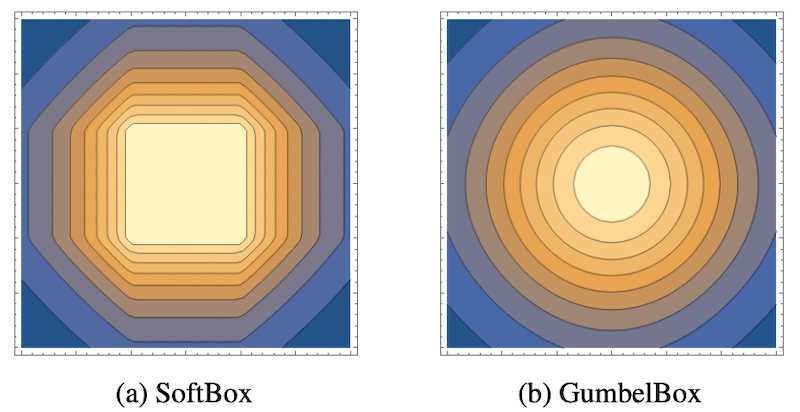
図は元論文の図8より引用しました。
この重なり方の違いが最適化時に違いを生み、平行移動に対する鈍感さなど Smoothed Box において最適化が難しかった場合に対処し、より適切に「箱」の位置を最適化することができます。
Dasgupta らは、Gumbel 分布に基づく Box Embedding の有効性を示すため、2次元の Gumbel Box と Smoothed Box を用いて可視化実験を行なっています。
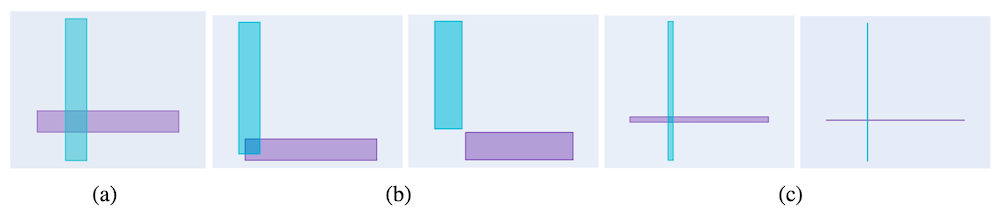
上の図は (a) で示される二つの交差した「箱」が与えられ、重なった領域を小さくするように学習した歳に、Gumbel Box と Smoothed Box がそれぞれどのように最適化を行うかの過程を示した図です。(b) の2枚の画像が Gumbel Box の最適化の過程を左から時系列順に示しており、(c) の2枚の画像が Smoothed Box の最適化の過程を左から時系列順に示しています。
(c) の Smoothed Box は、それぞれの「箱」の重なりを小さくすることには成功していますが、それぞれの箱自体が不必要に小さくなってしまっており、また完全に重ならないように箱を配置することにも失敗しています。
一方で、Dasgupta らが提案した Gumbel Boxでは、「箱」同士の重なりが徐々に小さくなっており、(b) の右側、すなわち学習が終わった段階で、それぞれの「箱」の大きさを保ちつつ、重なりを排除することに成功しています。
この例は「箱」同士の一部が重なっている場合でしたが、次は片方の「箱」にもう片方の「箱」が完全に含まれている場合についても見てみましょう。
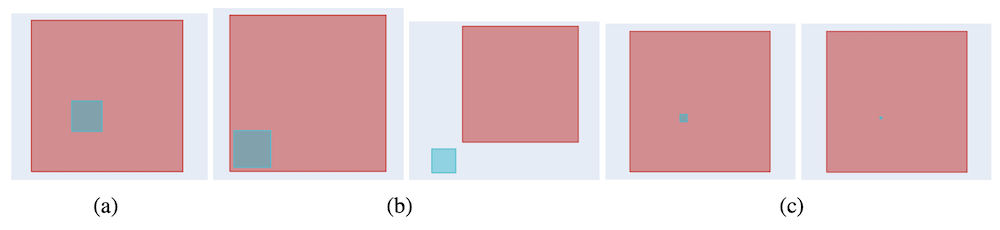
上の図は、先ほどと同様、(a) で示される二つの「箱」が与えられ、重なった領域を小さくするように学習を行った際に、Gumbel Box と Smoothed Box がそれぞれどのように最適化を行うかという過程を示した図です。
形式も先ほどと同様、(b) の2枚の画像が Gumbel Box の最適化の過程を左から時系列順に示しており、(c) の2枚の画像が Smoothed Box の最適化の過程を左から時系列順に示しています。
こちらの例でも、(b) で示されるように Gumbel Box は「箱」の大きさをほとんど変えないまま重なりを小さくできている一方で、(c) で示されるように Smoothed Box は「箱」自体が小さくなってしまっており、重なりを排除することにも失敗しています。
Dasgupta らは、このような定性的な観察に加えて、実世界の階層構造を表現したデータを用いた実験として、WordNet に含まれる名詞の階層関係予測タスクと、MovieLens データセットを用いた映画の選択選好予測タスクで Gumbel Box の有効性を評価しました。
実験の結果、Box Lattice や Smoothed Box といった既存手法を上回り、良好な性能を達成しました。
Word2Box
元論文: Dasgupta et al., ACL 2022. Word2Box: Capturing Set-Theoretic Semantics of Words using Box Embeddings
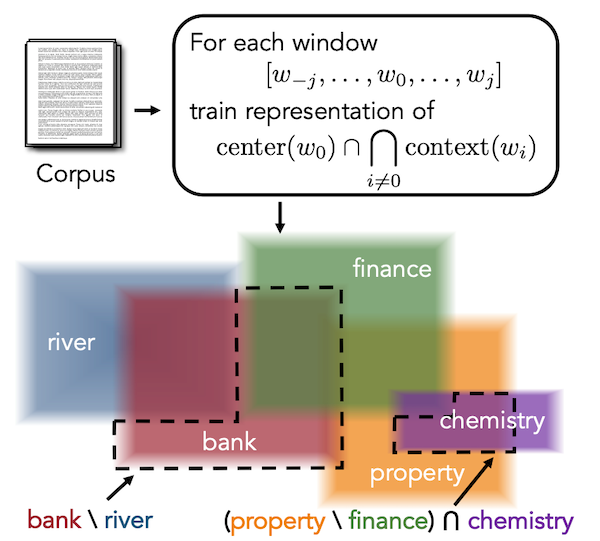
Gumbel Box の著者である Dasgupta らが提案した Word2Box は、これまでに説明してきた Box Embedding の技術を用いて、教師なし学習によって単語の Box Embedding を獲得する手法です。
これまでの Box Embedding 手法は教師データを用いて「箱」同士の重なり具合を最適化していましたが、Word2Box ではテキストコーパスから、Mikolov らが提案したWord2Vec のアルゴリズムである CBOW と同様のアイデアによって、ある単語とその周辺に出現する単語をペアとして学習データを抽出します。
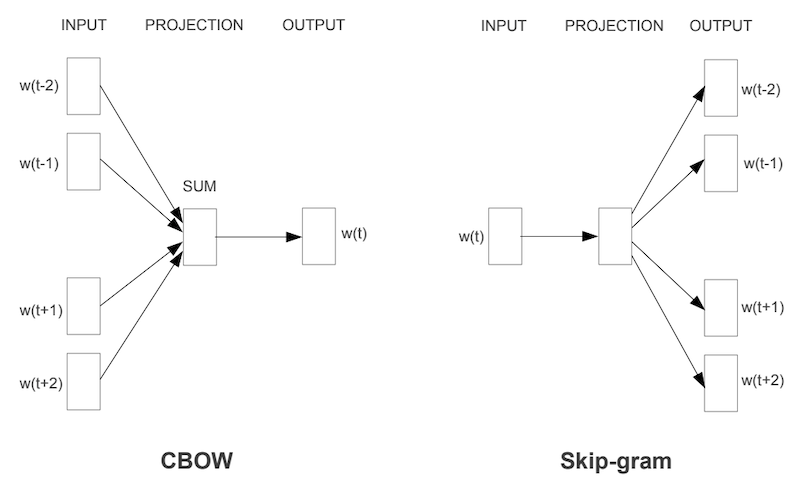
以下に CBOW と Skip-gram の概念図を示します。図は Mikolov et al. 2013 からの引用です。
元論文では曖昧な集合である Fuzzy set に基づく議論をもとに目的関数が設計されていますが、本記事では Word2Box の著者実装をもとに、より具体的に Word2Box の訓練について説明します。
Word2Box の訓練では、まずテキストコーパスからある単語を選びます。この単語を中心語 (center word) と呼びます。次に、その単語のある範囲までの単語を集めます。このように収集された単語を文脈語 (context word) と呼びます。また、文脈語を収集する際に、中心語からどの程度離れるかの距離を窓幅 (window size) と呼びます。
そして、中心語と文脈語をそれぞれ Box Embedding に変換し、この中心語と文脈語の「箱」の重なり度合いが大きくなるように学習を行います。この重なり度合いの計算には Gumbel Box と同様に「箱」の交差部分の体積を Gumbel 分布に基づいて計算します。
ここで、中心語と文脈語の体積を大きくするだけでは、何も考えずすべての「箱」を大きくすれば良いことになってしまうので、Mikolov らの Word2Vec と同様に、適当な単語をサンプリングして負例とします。
最後に、この負例単語と文脈語の「箱」の重なり度合いが小さくなるように学習を行います。
以上の説明を総括すると、Word2Box の訓練は Word2Vec における学習過程を Box Embedding によってアップデートしたものと言えそうです。
より具体的には、Word2Vec では単語のベクトル表現同士の類似度としてベクトルの内積が用いられていたところを、Word2Box では Gumbel Box による交差部分の体積に置き換えているものと考えることができます。
Word2Box のアイデアについて述べたところで、次に評価実験について述べます。
実験には、9億語規模の前処理済み英語テキストを用いて、64 次元の Word2Box を 10 エポック訓練し、評価に用いています。比較対象としては、同じテキストを用いて訓練された 128 次元の Word2Vec が用いられています。Word2Vec の次元数が Word2Box の2倍なのは、Word2Box が1つの次元ごとに始点と終点の2つのパラメータを持つため、表現のパラメータ数に関して公平な実験をするためです。
評価に用いるタスクは、大きく分けて単語類似度評価タスクと集合論的演算評価タスクの2つです。
まず、単語の表現の品質を評価するためのタスクである、単語類似度評価タスクを用いた実験について述べます。
このタスクは、単語のペアと、人手でアノテーションされた単語ペアの類似度が与えられた時に、モデルによって計算した単語ペアの類似度が、人手評価とどの程度相関するかを評価するタスクです。
実験では、単語類似度評価データセットとして有名な SimLex-999 などのベンチマークデータセットを用い、各モデルによって計算された類似度と人手評価とのスピアマンの順位相関係数を評価指標としています。
実験の結果を以下に示します。

ここで、表の各行は評価に用いたそれぞれのモデルを示し、各列は評価に用いるデータセットを示します。表の最も下の行に太字で示されるように、Word2Box の性能ははおおむね Word2Vec の性能を上回っていることがわかります。また、詳しい分析の結果、比較的希少語が多いデータセットでの性能向上が顕著であることも報告されています。
次の集合論的演算評価タスクでは、Word2Box の数値的な良さを評価する定量評価と、Word2Box の性質について実例を交えて評価する定性評価を行なっています。
実験の結果、Word2Vecのように単語を「点」で表現する手法よりも、単語を「箱」で表現する Word2Box の方が、多義語の扱いや「意味の引き算」の扱いがより適切であったとのことです。
まとめ
データを「点」ではなく「箱」で表現する Box Embedding について紹介し、教師なし学習によって単語の Box Embedding を獲得する Word2Box と呼ばれる手法を中心に、Box Embedding の基礎知識について解説しました。
単語のように複数の概念や意味を持ちうるデータの表現形式として、広がりを自然に表現できる「箱」を選択するのは将来性のある方向に見えます。
領域表現としては、データをガウス分布で表現したり、双曲空間上で表現したりといったことも考えられますが、Box Embedding には「箱」の交差や、交差部分の体積が簡単に計算できるという利点があります。
Box Embedding については著者らによるオープンソースの実装とライブラリの紹介論文が公開されており、実装を参考に考察・拡張しやすいのも嬉しいところです。
Box Embedding に関する研究はまだ発展途上であり、今後さらに大規模に学習された高次元の事前学習済み Box Embedding や、Box Embedding ベースの言語モデルなどが登場するかもしれません。
また、Box Embedding の多様なタスクへの応用も将来有望な方向性の一つでしょう。
大規模事前学習モデルの研究が盛んな昨今ですが、だからこそ一風変わった研究として、Box Embedding をはじめするデータを「点」以外の様々な形式で表現する研究が盛り上がっていくかもしれません。今後の動向にも注目です。
文責:塚越 駿(名古屋大学)
関連記事