先週、テキストから画像を高い品質で生成できるモデル DALL·E 2 が OpenAI から発表されました。現実にはあり得ないようなテキストから画像を生成できるその万能さと生成品質で世間を賑わせた初代「DALL·E」ですが、そこから一年ほどで、さらにテキストに忠実でリアルな画像生成が実現したことになります。
本記事では、「DALL·E 2」の技術詳細に注目し、論文を理解するための基礎となる技術を順に追って解説します。具体的には、
- CLIP
- 拡散モデル
- GLIDE
- DALL·E 2
の順に解説します。
ステート・オブ・AI ガイドでは、人工知能・機械学習分野の最新動向についての高品質な記事を毎月5〜6本配信しています。購読などの詳細につきましては、こちらをご覧ください。また、Twitter アカウントの方でも情報を発信しています。
画像とテキストの関連をとらえる CLIP とその応用
元論文: Radford et al., 2021. Learning Transferable Visual Models From Natural Language Supervision
まず、CLIP の概要を簡単におさらいしておきたいと思います。
CLIP は、画像エンコーダーとテキストエンコーダーから構成されており、テキストと画像の対応関係をとらえるモデルです。例えば、ソファーに横たわっている猫の画像(を埋め込んだもの)と「ソファーに横たわる猫」というテキスト(を埋め込んだもの)を与えると、その両者の類似度が高い、と判断するようなモデルです。まったく無関係の組み合わせであれば、逆に類似度は低くなります。
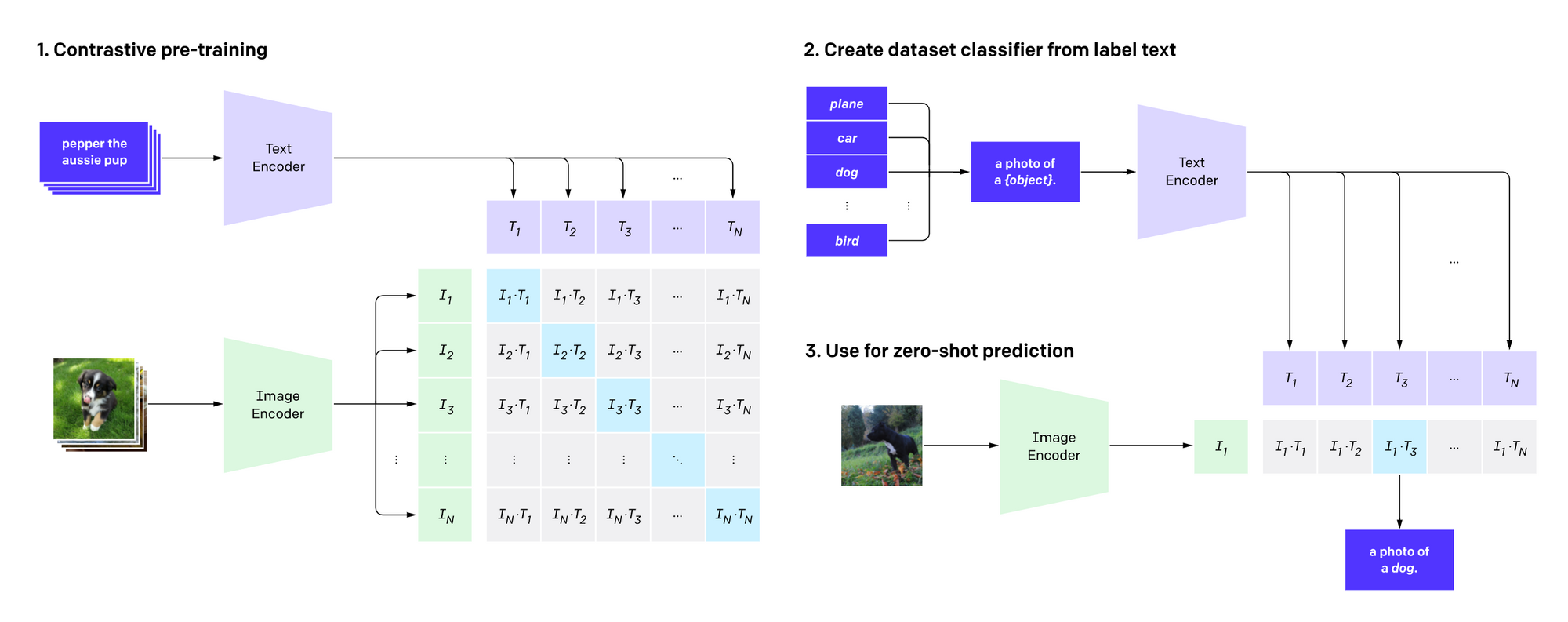
CLIP の訓練では、ウェブから豊富に取得できる大量の画像と、それらに結び付けられたテキストを使って、画像とテキストの対応モデルを事前学習します。具体的には、WebImageText と呼ばれる、ウェブから収集した「画像+テキスト」4億組を訓練データとして用いています。損失関数としては、画像から、その画像に対応する真の記述文を、ランダムに選ばれた他の記述文の中から見つけだす、という対照学習的な設定が使われています。
CLIP を使うと、対象タスクに対する微調整を全く経ずに予測する「ゼロショット学習」が可能になります。具体的には、例えば画像分類タスクに適用する場合、ある画像を画像エンコーダーに入力し、一方、「犬の写真」「猫の写真」のような記述文を人為的に作り、テキストエンコーダーに入力、その中でモデルの出す確率の最も高いクラスを選ぶ、という方法を使うことができます。これによって、特殊な分野のデータセットに対しても、非常に高い分類性能を発揮するということです。
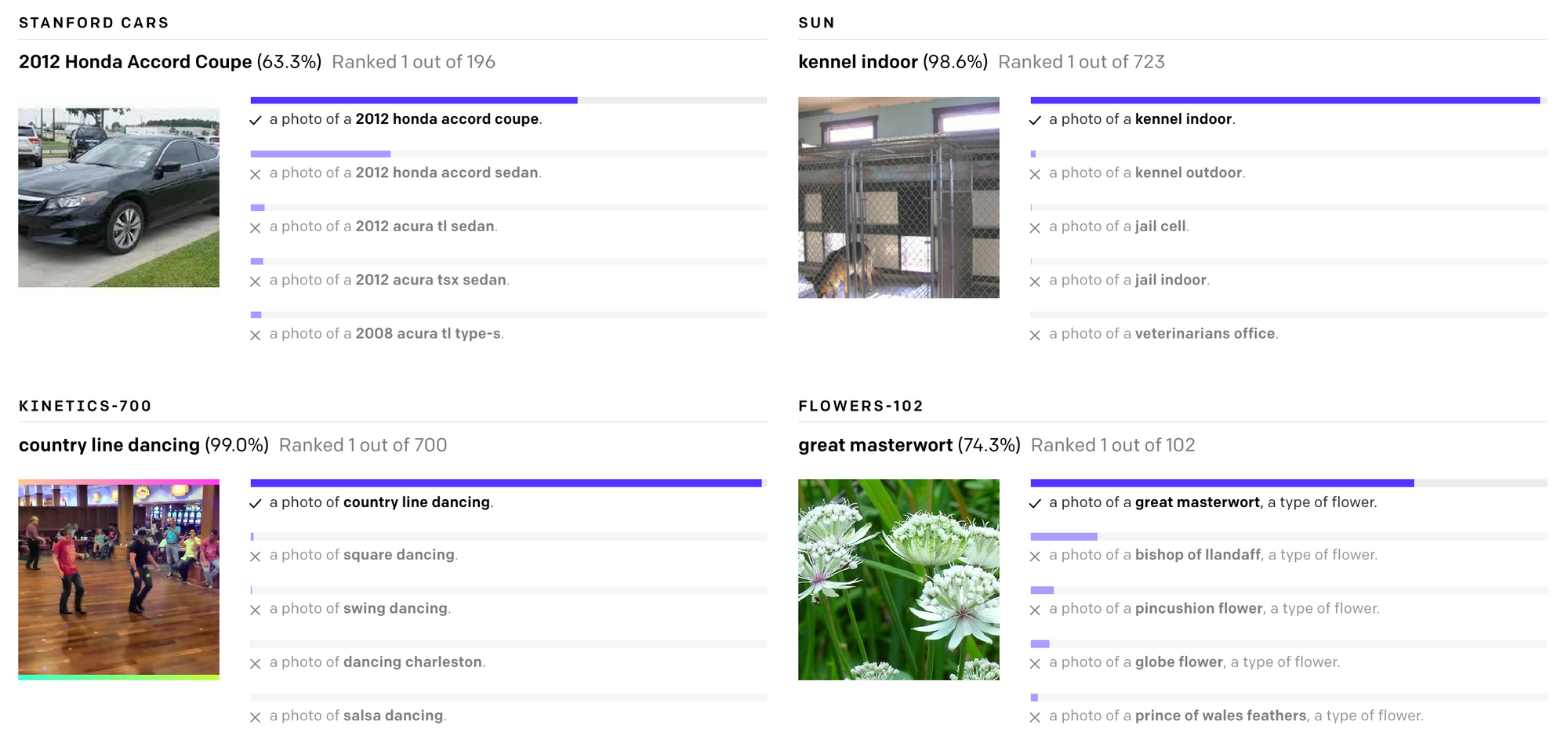
ImageNet の訓練データを全く用いることなしに、ImageNet で訓練した ResNet50 とほぼ同等の性能を出すということです。また、上の図から分かるように、様々なドメインのデータセットにおいて、そのデータセットで訓練することなしに正しく画像を分類することができます。
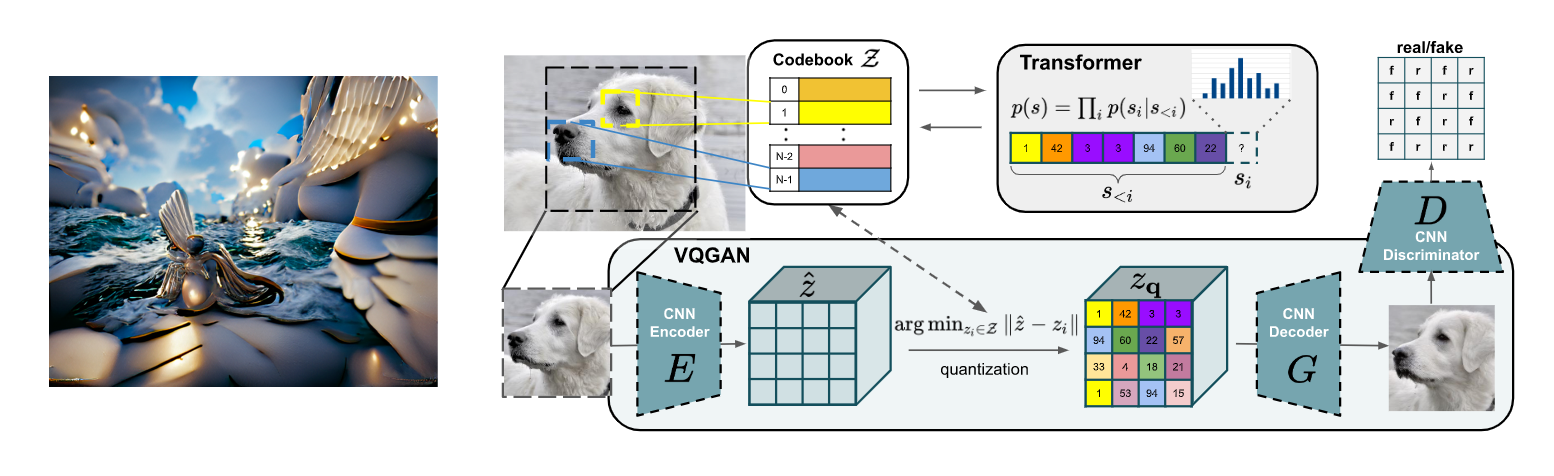
CLIP は、非常に強力なマルチモーダル・モデルであり、その後、様々なタスクや分野で応用が広がっています。最も有名なのは、CLIP と高画質な画像生成モデルである VQGAN (Esser et al., 2020) を組み合わせた CLIP+VQGAN によるテキストからの画像生成モデルでしょう。昨年の夏ごとに話題になり、ネット上には本モデルで生成した高画質な画像が溢れました (上図参照)。こちらの詳細については、以前の解説記事をご参照ください。
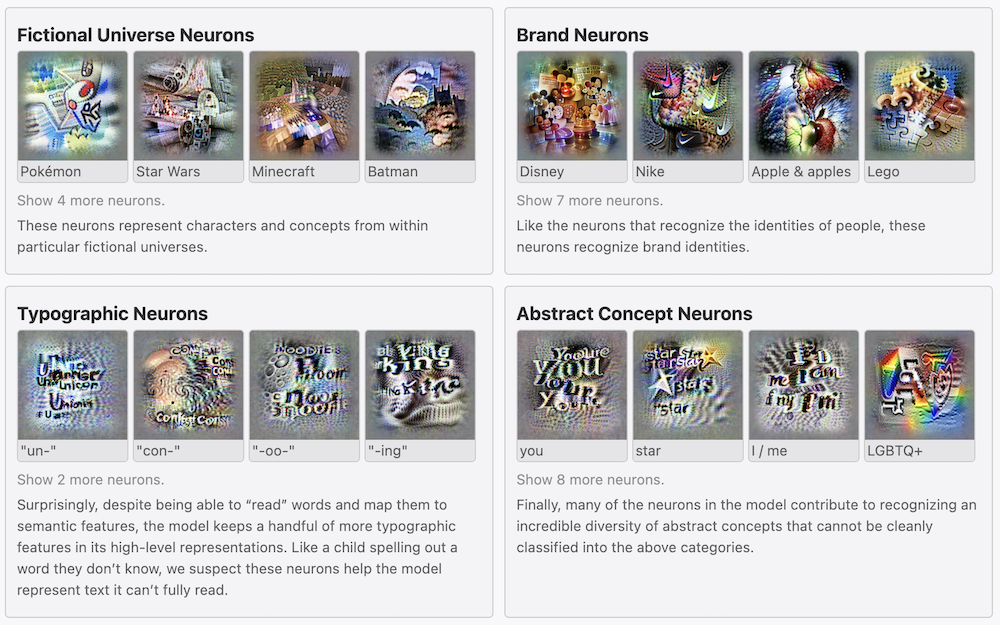
その他にも、CLIP がどのように画像やテキストを「認識」しているかという分析も進んでいます。例えば、OpenAI の研究者らは、詳細な可視化・分析を通じて、CLIP で学習されたニューロンの中に、人の顔や色など、画像の特徴をとらえるものに加え、文字や概念に反応するなど、マルチモーダル的な認識をするものがあることを突き止めています (Goh et al., 2021)。
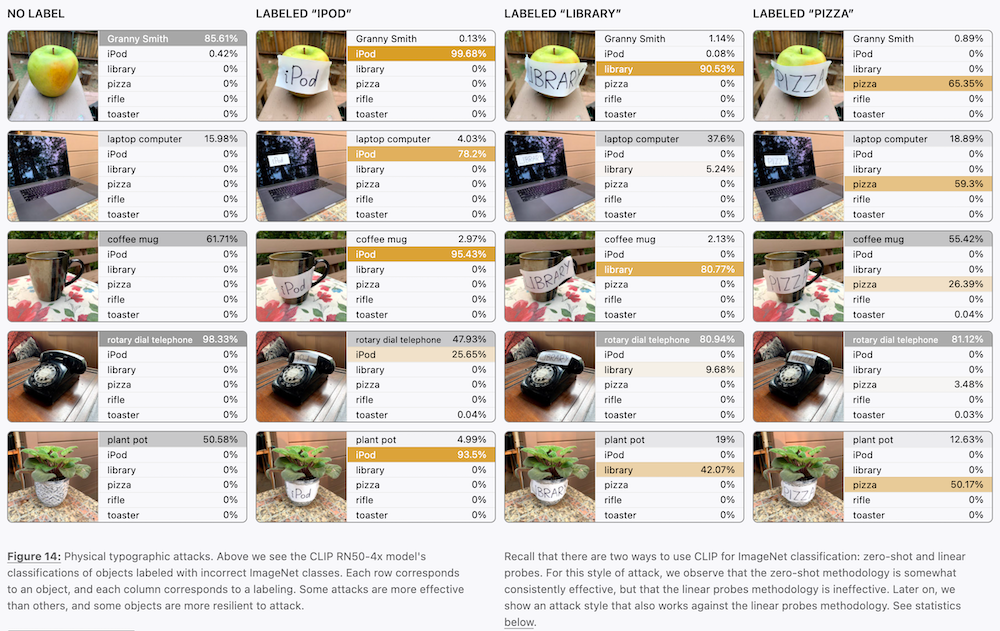
この性質を逆手に取って、画像に関係の無い文字を埋め込むことによって、CLIP ベースの画像認識モデルをだます「活字アタック (typographic attack)」も検討されています。例えば上の図では、リンゴの画像に対して、"iPod" という全く関係の無いテキストが書かれた紙を貼り付けることによって、画像が iPod であるという確率を大幅に上げられることが分かっています。
ノイズを除去しながらデータを生成する拡散モデル
元論文: Ho et al., 2020. Denoising Diffusion Probabilistic Models
この論文において提案された「ノイズ除去拡散確率モデル」(DDPM; denoising diffusion probabilistic models)。拡散モデルを使って高品質な画像生成が可能であることを最初に示した紀念碑的な重要な論文であると言えます。以前の記事でも解説しましたが、以下では、このモデルの基礎を簡単におさらいしておきましょう。
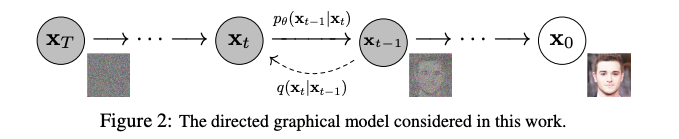
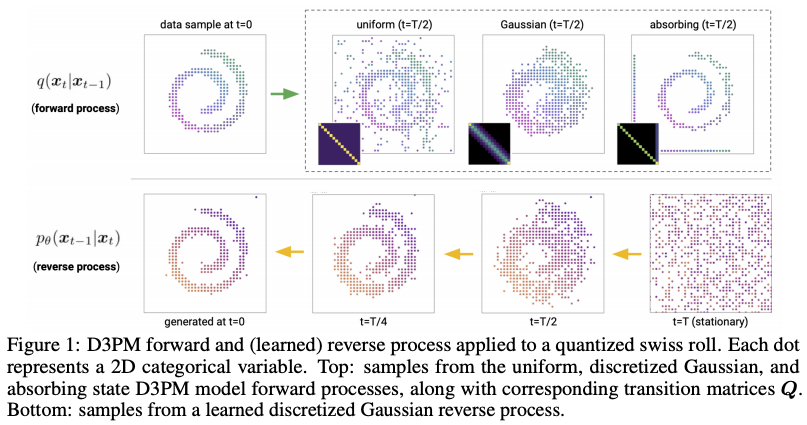
拡散確率モデル(以下、単に「拡散モデル」と呼ぶ)は、簡単に言うと、データに徐々にノイズを与えていくマルコフ過程モデルです。最初のデータ ${\bf x}_0$ に対してガウシアンノイズを何回も付加していくと、最後には元のデータが全く識別できないようなノイズ ${\bf x}_T$ になります。これを「前向き過程」や「拡散過程」と呼び、上の図では左向きの矢印が相当します。現在のデータ ${\bf x}_{t-1}$ に対して、ガウシアンによって以下のようにノイズを付与して、次のデータ ${\bf x}_t$ を求めます。
$$
q({\bf x}_t | {\bf x}_{t-1}) = {\cal N}({\bf x}_t; \sqrt{1-\beta_t} {\bf x}_{t-1}, \beta_t {\bf I})
$$
ここで、$\beta_1, ..., \beta_T$ は、ハイパーパラメータとしてあらかじめ設定された、時刻 $t$ におけるノイズレベル (ガウシアンの分散) です。
逆に、ノイズを除去し元のデータを復元するのが「後ろ向き過程」であり、現在のデータ ${\bf x}_t$ から、そのノイズを除去した、一段回前のデータ ${\bf x}_{t-1}$ を推定します。これは、上の図では右向きの矢印に相当します。以下のように、ノイズ除去後の平均と共分散を、現在のデータから関数 ${\bf \mu}_\theta({\bf x}_t, t)$ と ${\bf \Sigma_\theta}({\bf x}_t, t)$ を使って推定するモデルです:
$$
p_\theta({\bf x}_{t-1} | {\bf x}_t) = {\cal N}({\bf x}_{t-1} ; {\bf \mu}_\theta({\bf x}_t, t), {\bf \Sigma_\theta}({\bf x}_t, t))
$$
この拡散モデルは、データの尤度を最大化させることによって学習します。この中間過程を全て潜在変数だと仮定すると、VAE などと同様に、変分下限 (VLB; variational lower bound) を最大化することによって学習が進みます。詳細な式は省略しますが、この損失関数の導出によって出てくる項は全てガウシアン間の KL ダイバージェンスであるため、解析的に求めることができます。
このあたりの理論的詳細は、実は Sohl-Dickstein らの 2015年の論文 によって既に示されています。詳細な式の導出もあるので、興味にある方はそちらを参照いただければと思います。
なお、本論文では、データを復元する後ろ向き過程において、現在のデータ ${\bf x}_t$ からノイズ除去後の分布の平均 ${\bf \mu}_\theta({\bf x}_t, t)$ を直接推定するのではなく、「どれだけ動かしたらノイズが除去できるか」という「差分」である ${\bf \epsilon}_\theta({\bf x}_t, t)$ を推定し、その差分を今のデータから引く、というパラメータの付け替え (reparametrization) をしています。こうすると、ある種の「どの方向に動かせば綺麗なデータの尤度が高まるか」という勾配を、関数(ニューラルネットワーク)によって求めていることになります。
この論文では、このように定義した拡散モデルが、以前から提案されていたスコアベースの生成モデル (Song and Ermon 2020) とほぼ等価であることを示しています。スコアベースの生成モデルについては、以前、本ブログでも解説記事を書きました ので、そちらを参考いただければと思います。
なお、Nichol 氏と Dhariwal 氏の最近の論文では、これまでハイパーパラメータとして固定されていたノイズレベル、すなわち、後ろ向き過程の分散 ${\bf \Sigma_\theta}({\bf x}_t, t)$ をパラメータ化し、損失関数の一つの項として追加。より少ないステップ数で、高画質な画像生成が可能になったということです。
誘導技術を使ってテキストからの画像生成を実現する GLIDE
GLIDE については、以前の記事でも関連論文と共に解説しましたので、そちらもご参照ください。
OpenAI によって発表された本論文 (Nichol et al., 2021) では、GLIDE (Guided Language to Image Diffusion for Generation and Editing) と呼ばれるモデルを提案し、テキスト条件付きの拡散モデルによって、リアルな画像が生成できるかどうかに挑戦しています。
GLIDE の特徴は、何らかの入力 (クラスやテキスト) を使って、拡散モデルの生成を誘導するという誘導拡散 (guided diffusion) の手法です。
クラスラベルを使って誘導するためには、拡散モデルによってノイズを徐々に除去する際に、分類器から出力されたクラス $y$ の対数確率 $\log p_\phi(y|x_t)$ の勾配を足し合わせ、以下のように、クラス確率が増加する方向に生成を「誘導する」ことができます。
$$
\hat \mu(x_t | y) = \mu_\theta (x_t) + s \cdot \Sigma_\theta(x_t | y) \nabla_{x_t} \log p_\phi(y | x_t)
$$
なお、ここで、$s$ は「誘導スケール (guidance scale)」と呼ばれ、誘導の強さをコントロールする重要なパラメータです。
GAN 等で識別器からの損失信号を使って生成器の訓練を誘導するプロセスに似ていますね。ただ、この方法だと、生成器とは別に分類器を訓練しなければならないという欠点があります。
そこで、最近になって、分類器フリーの手法 (Ho and Salimans, 2021) が提案されています。ここでは、分類器を別に訓練するのではなく、クラスによって条件付けた拡散モデル $\epsilon_\theta (x_t | y)$ を考えます。訓練する際に、一定の確率で、このラベル $y$ を「空ラベル」 $\emptyset$ によって置き換え、クラス条件の無い拡散モデル $\epsilon_\theta (x_t | \emptyset)$ も同時に訓練しておきます。生成の際には、$\epsilon_\theta (x_t | y) - \epsilon_\theta (x_t | \emptyset)$ を誘導に使うことによって、以下のように、分類器無しでクラス誘導が実現できます:
$$
\hat \epsilon_\theta(x_t | y) = \epsilon_\theta(x_t | y) + s \cdot (\epsilon_\theta (x_t | y) - \epsilon_\theta (x_t | \emptyset))
$$
この手法は、$y$ がクラスラベルではなく、テキストであっても同様に実装ができます (一定の確率で、テキストを「空テキスト」で置き換えれば良い)。

分類器フリーの GLIDE によって生成された画像の例を上にいくつか示します。「電卓を使うハリネズミ」「赤い蝶ネクタイと紫のパーティー帽子をかぶったコーギー」など、現実にあり得そうもない概念の組み合わせでも、テキストに忠実かつ高品質な画像が生成できていることが分かります。実験では、上述の分類器フリーの誘導手法と、CLIP (Radford et al., 2021) を使って誘導した方法では、前者の分類器フリーの誘導手法の方が、人間による評価で高いスコアを達成しており、その質は、1年ほど前に出て世間を賑わせた画像生成モデル DALL·E をも上回り、87% の場合で、GLIDE の出力が、人間にとって好ましいと判断されたということです。
2段階の拡散モデルで高品質の画像生成を達成した DALL·E 2
公式ブログ記事: https://openai.com/dall-e-2/
論文: Ramesh et al., 2022. Hierarchical Text-Conditional Image Generation with CLIP Latents
ここでついに、最近 OpenAI から発表された高品質画像生成モデルの DALL·E 2 の技術詳細を見ていくことにしましょう。なお、その生成された画像などについての一般的な話は、インターネット上に多数の記事がある (例えば、ITmedia や GIGAZINE) ので、そちらをご覧いただくとして、本記事では技術的な詳細に注目します。
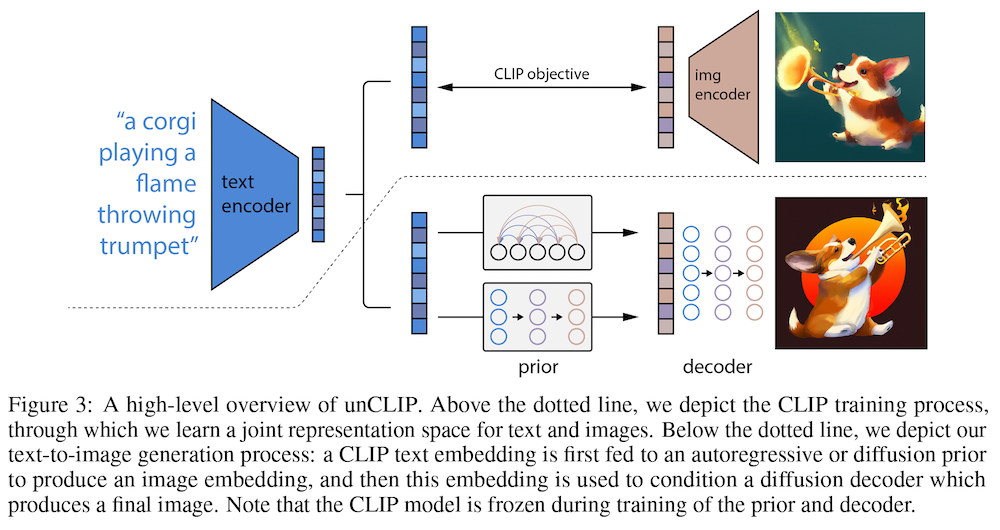
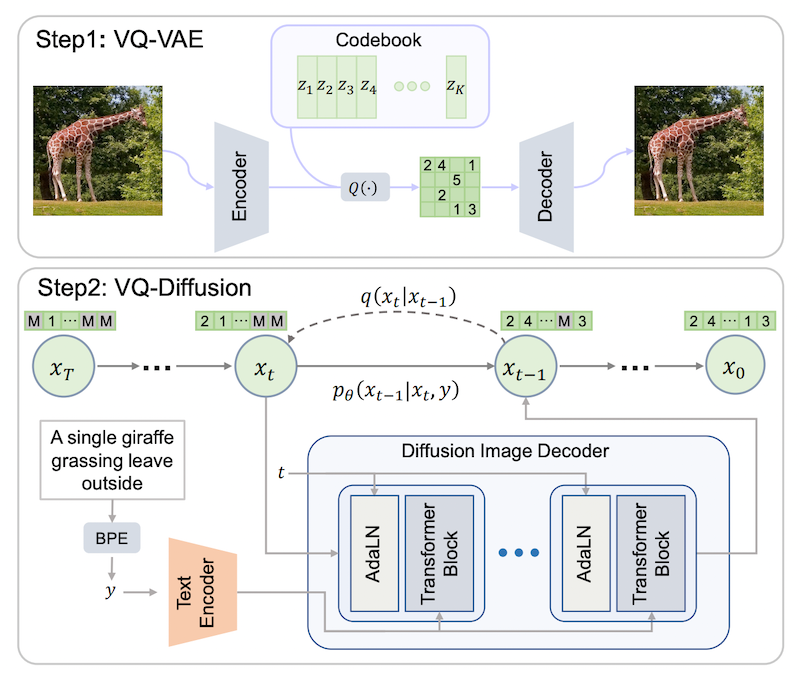
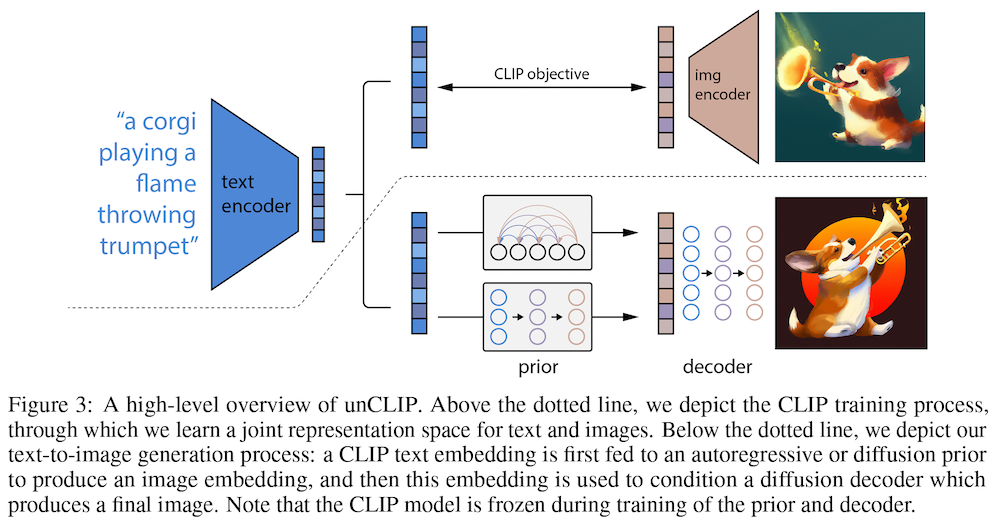
DALL·E 2 は、一言で言うと、CLIP と拡散モデルベースの画像生成を組み合わせた2段階モデルです。上図の下に示したように、
- 画像の埋め込みを生成する「事前分布 (prior)」
- 埋め込みから画像自体を生成する「デコーダー (decoder)」
の2つのコンポーネントの組み合わせで構成されています。
まず、「事前分布」は、テキスト・キャプション (自然言語による記述文) から CLIP の画像埋め込みを生成します。$y$ をテキスト・キャプション、$z_i$ を CLIP の画像埋め込みとすると、$P(z_i | y)$ をモデル化していることになります。
この「事前分布」のために、論文では、以下の2つのアプローチを試しています。
- 自己回帰的なモデル: $z_i$ を離散トークンの系列に変換し、自己回帰的に予測
- 拡散モデル: 連続的な $z_i$ をガウシアン拡散モデルを使って生成。具体的には、ノイズの乗った画像埋め込みから、ノイズの無い画像埋め込み、を予測します。テキストと、テキスト埋め込みを条件付けに使います。
実験の節でも述べますが、このうち、拡散モデルを使った方が、画像生成の質が高かったということです。
次に、「デコーダー」は、CLIP 画像埋め込みから画像を生成します。元の CLIP の画像エンコーダーは、画像を受け取って埋め込みを生成するので、ここでは「CLIP を反転」しているものだと考えればよいでしょう。$x$ を生成画像だとすると、ここでは $P(x | z_i, y)$ をモデル化していることになります。
このデコーダーは、上記の GLIDE とほぼ同じ 3.5B (35億) パラメータのテキスト条件付き拡散モデルを使っています。分類器フリーの誘導手法 (Ho and Salimans, 2021) を使っている点も同じです。最初に、64 × 64 ピクセルの画像を生成し、それを高解像モデル ADMNet (Dhariwal and Nichol, 2021) を使って 256 ピクセル、次に 1,024 ピクセルの画像に高解像化します。
論文では、この「事前分布+デコーダー」の組み合わせを "unCLIP" と呼んでいます。この事前分布の訓練には CLIP と DALL-E の訓練データを組み合わせたものを、デコーダーの訓練には、DALL-E の訓練データと同じものを使っているということです。
ちなみに、テキストから画像の生成だけを考えるのであれば、事前分布は厳密には必要無い点に注意する必要があります。2段階目のデコーダーに直接、テキストの情報を条件付けとして入力できるからです。ただ、Fréchet Inception Distance (FID) (Heusel et al. 2017) 値で比較すると、unCLIP の2段階モデルが最も良い性能を示したということで、以下の評価ではこの「拡散モデルによる事前分布+拡散モデルによるデコーダー」の組み合わせを使っています。
DALL·E 2 の評価はいかに

DALL·E 2 は「CLIP を反転」できることから、この性質を使って、画像の「バリエーション」を生成できるという特徴があります。具体的には、画像から、通常の CLIP の画像エンコーダーを使って埋め込み $z_i$ を生成、それをデコーダーを使って「反転」させるというものです。これによって、上図のように、画像の「意味」やスタイルを保ったまま、詳細の異なる画像を複数生成することが可能になります。

また、上図のように、2つの画像の埋め込みを補間し、そこから画像をデコーダーで生成することによって、画像の内容を徐々に、自然に変化させることが可能です。

さらに、上述の「活字アタック」をされた画像に対しても、「バリエーション」を生成すると、iPod ではなくリンゴの画像をきちんと生成できます。ここから、アタック後も、画像の重要な情報は埋め込みとしてエンコードされていることが分かります。

また、著者らは、CLIP 画像埋め込みに対して主成分分析 (PCA) を適用し、いくつかの主成分のみを残して画像を復元した時の画像の様子を観察しています。残す主成分の数が少ない場合 (上図左側) 、「料理」「街」「草原」などの大まかな情報しかとらえられませんが、残す主成分の数が増える (上図右側) にしたがい、物体の数や位置などの情報が少しずつ復元できていることが分かります。
評価実験では、生成画像の (写真のような) リアリティと、多様性を、人手によるペアワイズ比較 (2つのモデルの結果を並べて提示して、どちらが良いかを答えてもらう) によって比較しています。自己回帰モデル (AR) より拡散モデルが、リアリティで同等もしくは少し上、また、多様性で大幅に上回るという結果になりました。

また、誘導スケール $s$ を変化させながら画像を生成した結果 (上図) を見ると、GLIDE では誘導が強くなるにつれ、画像がどれも似通ったものになり、多様性が無くなるのに比べ、本手法 unCLIP では、画像生成の質を保ちながら、さらに高い多様性を実現できていることが分かります。
MS-COCO の検証セットを使い、ゼロショットで(MS-COCO の訓練データを使わずに)画像生成した結果では、画像生成の質で SOTA を達成したということです。
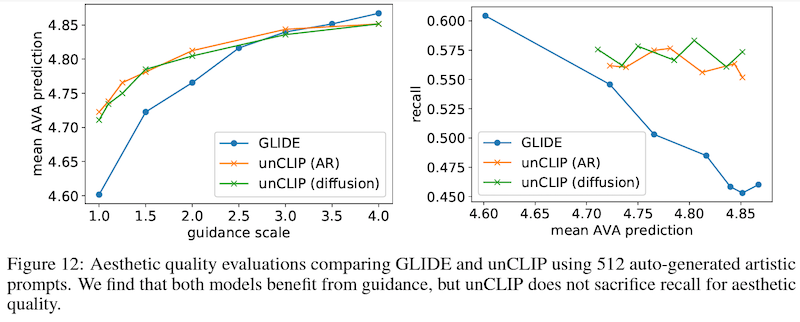
最後に、生成画像の「美しさ」に関する評価です。ここでは、人手で全て評価をするのは大変なので、CLIP の画像埋め込みから線形モデルによって「美しさ」の人手評価を予測するモデルを訓練しています。上のグラフ (左側) で示したように、GLIDE と同様に、誘導の強さを上げることによって「美しさ」評価は向上しますが、上のグラフ (右側) で示されているように、GLIDE と比べて多様性をより高いレベルで保てることを示しています。

最後に、本モデル unCLIP の問題点・限界も指摘されています。例えば、「青い立方体の上に赤い立方体が乗っている」という入力では、GLIDE に比べて一貫性のある結果が生成できませんでした。また、「deep learning と書かれた標識」という入力では、上の図のように、一貫したテキストの生成に難があることも分かっています。CLIP の埋め込みに文字レベルの情報まで完全にエンコードされていない可能性に加え、低解像度から高解像度の画像を生成する仕組みにも一因がある可能性があ指摘されています。
おわりに
どのようなテキスト入力に対しても生成できる万能さと、その画像生成の質でネットを賑わした DALL·E 2 ですが、技術的な背景を追ってみると、まず CLIP があり、そこに、拡散モデル → GLIDE → DALL·E 2 という、地道な技術の進歩があったことが分かります。この背景にあるのは「拡散モデル」の発展であり、コンピューター・ビジョンだけではなく、言語 (Austin et al., 2021) や音声 (Kong et al., 2020) など他のドメインでの生成の質の向上も期待できそうです。
関連記事