深層学習のあらゆるタスクで使われているトランスフォーマー。非常に強力なモデルですが、レイヤーの数を増やしていくと訓練が不安定になることが知られています。最近、Microsoft Research から発表された本論文では、数行のコードで実装できる非常にシンプルな変更を加えるだけで、トランスフォーマーの訓練を安定させ、1,000層にも及ぶ「超深層トランスフォーマー」の訓練を可能にする DeepNet が提案されており、機械翻訳タスクにおいて目覚ましい性能を上げ話題となっています。系列変換モデルだけではなく、GPT 的な言語モデルなど、幅広い機械学習タスクに適用して改善できる可能性を秘めており要注目の本論文。本記事では、DeepNet とその正規化手法である DeepNorm を、論文速報として解説します。

ステート・オブ・AI ガイドでは、人工知能・機械学習分野の最新動向についての高品質な記事を毎月5〜6本配信しています。購読などの詳細につきましては、こちらをご覧ください。また、Twitter アカウントの方でも情報を発信しています。

元論文: Wang et al., 2022. DeepNet: Scaling Transformers to 1,000 Layers

トランスフォーマーの正規化・残差接続のおさらい

まず、DeepNet の解説に入る前に、トランスフォーマーのアーキテクチャ、特に、そのサブレイヤーの正規化と残差接続について、簡単におさらいしておきます。

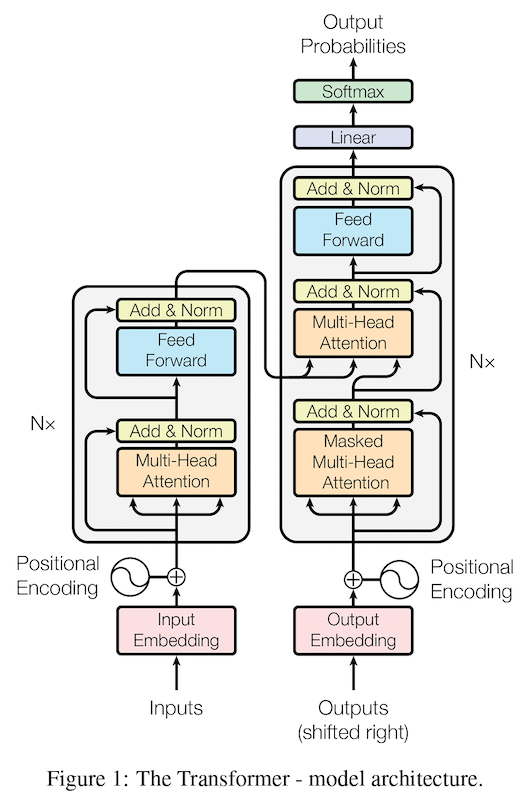
transformer

上の図に示した通り、トランスフォーマーの各レイヤーは、(1) 自己注意機構および (2) 順方向伝播 (feed forward) の２つのサブレイヤーから構成されます。自己注意機構は、以下の演算を適用します:

$$
{\rm Attn}(Q, K, V) = {\rm softmax}\left(\frac{QW^Q(KW^K)^T}{\sqrt{d_k}}\right)VW^VW^O
$$

ここで、$W^V$ と $W^O$ は、値 (バリュー) $V$ と全体の出力をそれぞれ投影する行列です。これらが以下の解説で重要になります。

サブレイヤーの演算を適用した後は、残差接続 (residual connection) によって演算を通過していない元の入力と足し合わせ、レイヤー正規化 (LayerNorm; LN) を適用します。

これを式で書くと、以下のようになります。

$$
x_{l+1} = LN(x_l + G_l(x_l, \theta_l))
$$

ここで、

  • $LN$ ... レイヤー正規化
  • $x_l$ ... $l$ 番目のサブレイヤーの入力
  • $\theta_l$ ... $l$ 番目のサブレイヤーのパラメータ
  • $G_l$ ... サブレイヤーの演算 (自己注意機構や順方向伝播層など)

を表しています。この構成は、元祖トランスフォーマーの論文 (Vaswani et al., 2017) で提案されたもので、サブレイヤーの演算の後にレイヤー正規化が適用されるため、Post-LN (Post-LayerNorm; 事後レイヤー正規化) と呼ばれます。

一方、サブレイヤーの演算の前にレイヤー正規化 (LayerNorm; LN) を適用する Pre-LN (事前レイヤー正規化) の構成もあります。同じように数式で書くと、以下のようになります。

$$
x_{l+1} = x_l + G_l(LN(x), \theta_l)
$$

この Pre-LN 構成は、GPT-2 (Radford et al., 2018) や GPT-3 (Brown et al., 2020) などにも使われており、訓練を安定させる効果があることが知られています (Nguyen and Salazar, 2019)。一方で、初期レイヤーの勾配が大きくなってしまい、性能が低下することが知られています (Shleifer et al., 2021)。

以上をまとめると、トランスフォーマーには、以下の２つの構成が存在します:

  • Post-LN (元祖) ... レイヤー正規化を残差接続「後」に適用。性能が高いが、訓練が不安定。
  • Pre-LN (改善型) ... レイヤー正規化を演算の「前」に適用。訓練が安定するが、同じ条件下では性能は Post-LN より低い

本記事で紹介する DeepNet およびその正規化手法である DeepNorm は、この Post-LN と Pre-LN の「いいとこ取り」をします。つまり、Post-LN のような性能を保ちつつ、Pre-LN のように訓練を安定させ、非常に深いトランスフォーマーの訓練を可能にするものです。

深いトランスフォーマーの不安定さ

論文ではまず最初に、通常の Post-LN トランスフォーマーの訓練が不安定であることと、その原因について詳細に調査しています。

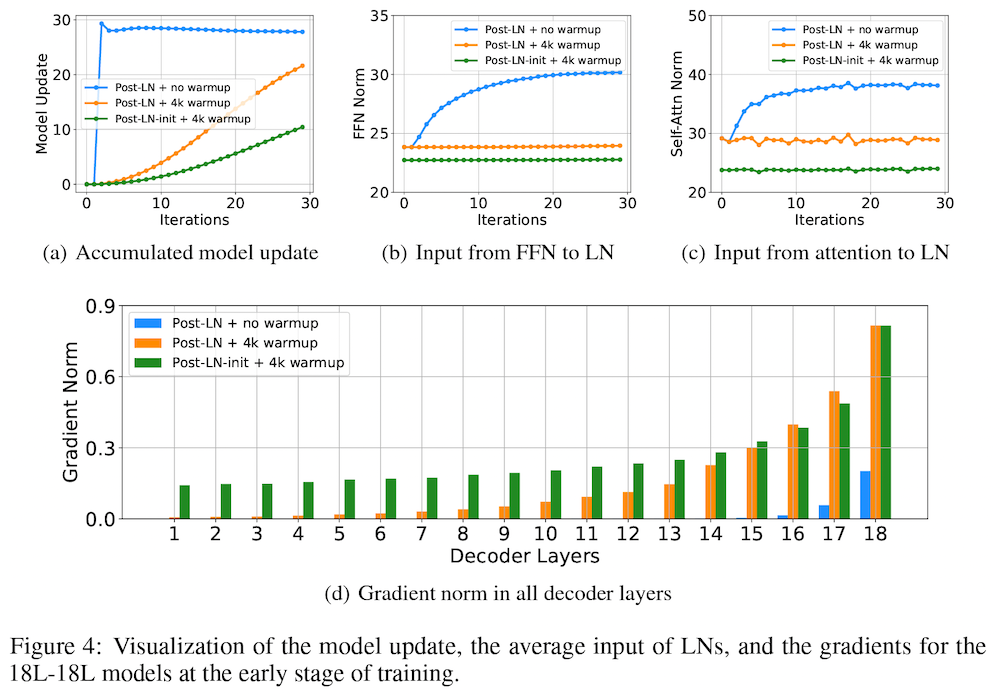
figure4

具体的には、まず、18レイヤーの通常の Post-LN トランスフォーマーを訓練させた場合、訓練が不安定であり、検証セットの損失関数の値（ロス）が収束しないことを示しています。このとき、「モデル更新量 (model update)」、すなわち、初期化時に比べて、モデルの更新後に、出力の値がどのぐらい変化したか、に注目すると、上図 Figure 4 の (a) の青線のように、学習の初期に爆発的に増え、その後ほとんど変化していないことが分かります。これは、学習の初期の段階で、モデルのパラメータが局所解に陥ってしまっている可能性を示唆しています。

このとき、レイヤー正規化層の入力の値に注目すると、上図 Figure 4 の (b) の青線のように大きくなっていることが分かります。レイヤー正規化を通る勾配の大きさは、入力の大きさに反比例することが知られている (Xiong et al., 2020) ので、これによって、上図 Figure 4 の (d) の青い棒グラフに示されたように、特に下位のレイヤーにおいて、勾配消失 (vanishing gradient) の問題が起きており、局所解から抜けられなくなっていることが示唆されます。

この問題は、これまで広く採用されている手法である、学習率を徐々に増やしていく「ウォームアップ」によってある程度軽減されることが分かります (上図 Figure 4 のオレンジの線)。また、著者らは、順方向伝播層の出力投影のパラメータを、低位レイヤーに対して小さく初期化する 「Post-LN-init」 と呼ばれる方法を提案し、これによってさらに学習が改善することを示しています (上図 Figure 4 の緑色のグラフ)。

この「自己注意機構の出力投影のパラメータを小さくする」というのが、以下で説明する DeepNet / DeepNorm の一つの着眼点となっています。

超深層トランスフォーマーの訓練を安定させる DeepNorm

本論文では、上の実験に着想を得て、モデル更新量をある一定に抑えるために、DeepNorm と呼ばれる新たな正規化手法を提案しています。DeepNorm の仕組みは、上記 Post-LN (オリジナルのトランスフォーマー) と非常に類似しています。数式で書くと、以下のようになります:

$$
x_{l+1} = LN(\alpha x_l + G_l(x_l, \theta_l))
$$

違いは、残差接続の値を $\alpha$ 倍して大きくすることです。また、パラメータの初期化時に、サブレイヤーの演算のパラメータ $\theta_l$ を $\beta$ 倍して小さくします。たったそれだけの変更で、超深層トランスフォーマーの訓練を安定させることができます。

この DeepNorm が学習を安定させる根拠として、論文では理論的裏付けを与えています。具体的には、上でも注目したモデル更新量

$$|| \Delta F ||$$

すなわち、初期化時に比べ、モデルの更新後に、出力の値がどのぐらい変化したか、という量に注目すると、最適化に SGD を使うという仮定の下、以下の関係が成り立つことを示しています:

$$
|| \Delta F || \le \sum^{2N}_{i=1} \frac{\sqrt{v_i^2 + w_i^2}}{\alpha} || \theta^*_i - \theta_i ||
$$

ここで、

  • $N$ ... レイヤー数
  • $v_i$ ... 自己注意機構の値 (バリュー) 射影行列 $W^V$ (をスカラーによって単純化したもの)
  • $w_i$ ... 自己注意機構の出力射影行列 $W^O$ (をスカラーによって単純化したもの)
  • $\theta^*_i, \theta_i$ ... 更新後および初期のパラメータ

です。

ここから、モデルは、各レイヤーごとに更新を蓄積していくため、レイヤー数が増えるに従ってこの量が爆発的に増加し、学習が不安定となる原因になっていることが分かります。また、モデル更新量 (左辺) を小さく保つには、右辺の

  • $\alpha$ を (総レイヤー数に比例させる形で) 大きくする
  • $\sqrt{v_i^2 + w_i^2}$ を (総レイヤー数に反比例させる形で) 小さくする

ことが有効であることが分かります。

論文では、エンコーダーとデコーダーから成り立つ系列変換トランスフォーマー・モデルについても同様の分析をしており、エンコーダーの更新量が、エンコーダー・デコーダーのレイヤーの数に比例して累積していくことを示しています。特に、クロス注意機構によってエンコーダーからデコーダーに大きさが伝播するので、デコーダーの方が学習が不安定になりやすいとのことです。同様の結果は、トランスフォーマーの訓練を安定させる手法 Admin を提案した Liu et al., 2020 でも示されています。

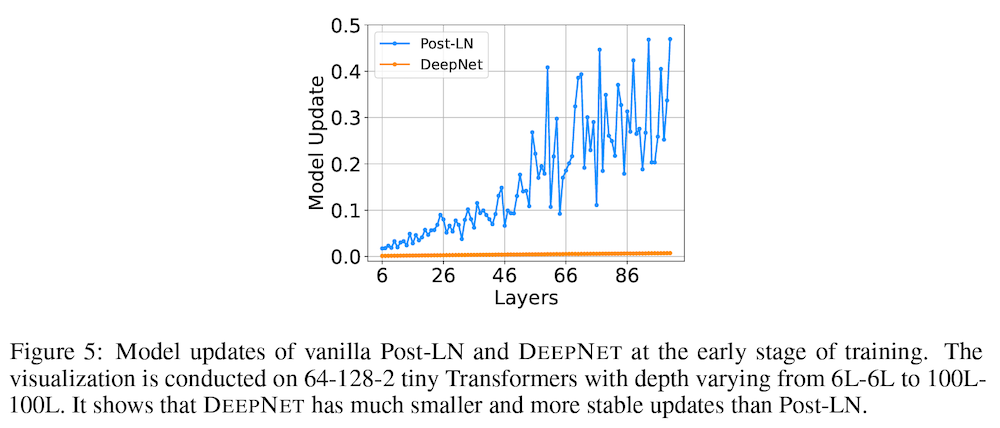
figure5

上の Figure 5 では、この問題を図示するために、元祖 Post-LN トランスフォーマーのレイヤー数を 6 層から 100 層まで変化させた時のモデル更新量をプロットしています。上の式から示唆されるように、レイヤー数が増えるほどモデル更新量が蓄積されている様子が読み取れます。

詳細な導出は省略しますが (興味のある方は、論文の 4.3 節をご覧ください)、このモデル更新量が、レイヤー数に依存せずに、学習率 $\eta$ のみによって決まる ($\Theta(\eta)$ によって漸近的におさえられる) ようにするには、上の不等式で出てきた $1 / \alpha^2$ と $v_i^2 + w_i^2$ の値を、レイヤー数に反比例するように設定すれば良いことが分かります。バランスを取って、値 (バリュー) の射影行列 $v_i$ の係数と出力射影行列 $w_i$ が同じ ($v = w = \beta$) であると仮定すると、

  • エンコーダー ... $\alpha_e = 0.81 (N^4 M) ^ \frac{1}{16} $, $\beta_e = 0.87 (N^4 M)^{-\frac{1}{16}}$
  • デコーダー ... $\alpha_d = (3M)^\frac{1}{4}$, $\beta_d = (12M)^{-\frac{1}{4}}$

という値に設定すれば良いことが分かります。$\alpha$ は 1 よりも大きく、$\beta$ は 1 よりも小さな値になることに注意してください。ここで、$\beta$ は、値 (バリュー) および出力投影行列のパラメータに対する係数ですが、パラメータの初期化時に、同じ係数をパラメータに掛け合わせて小さくすることによって、同様の効果が期待できます。

figure2

以上をまとめると、DeepNorm は、上図 Figure 2 のように、

  • サブレイヤー内の残差接続を $\alpha$ 倍して大きくする
  • 順方向伝播層および自己注意機構の値 (バリュー) と出力投影行列を Xavier 初期化 (Glorot and Bengio, 2010) する際に、$\beta$ 倍して小さくする
  • 一方、クエリとキーの投影行列はモデル更新量に影響を与えないので、そのままにする
  • 定数 $\alpha$ と $\beta$ は、アーキテクチャとレイヤー数に応じて、上図右のように設定する

だけで、コード量にして数行で実現できることが分かります。

機械翻訳モデルによる DeepNet の検証

実験では、機械翻訳における標準的なデータセットである WMT-17 (英語-ドイツ語) を使い、機械翻訳に良く使われる評価指標 BLEU に基づき、DeepNorm を使ったトランスフォーマーモデルである DeepNet の性能検証をしています。

ベースラインとして、元祖トランスフォーマー (Vaswani et al., 2017) の Post-LN と Pre-NL の両構成、および、これまでに紹介した NormFormer (Shleifer et al., 2021) や Admin (Liu et al., 2020) などのトランスフォーマーの改善手法と比較しています。

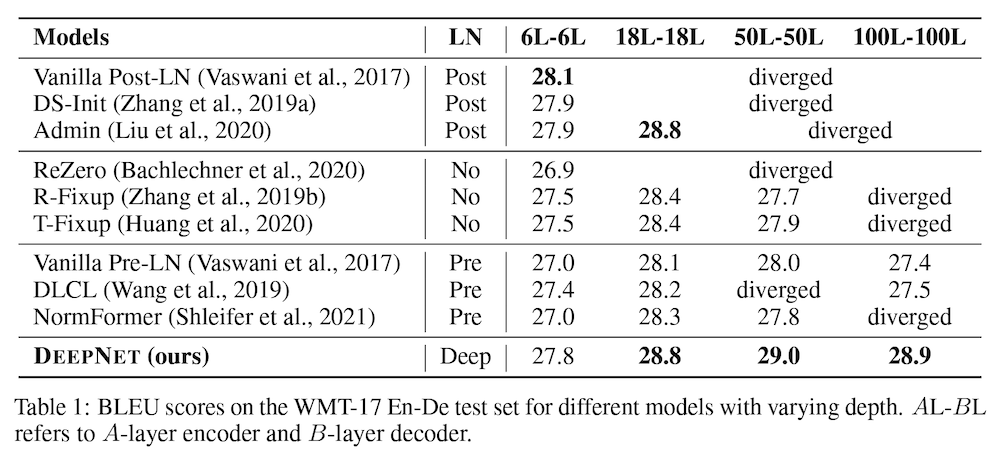
table1

上の表 (Table1) に示したように、他のベースラインでは、学習が発散 (diverged) してしまったり、レイヤー数を増やしても性能が向上しなかったりといった結果を示した一方で、提案手法である DeepNet (最下段) は、100レイヤーまで増やしても訓練が安定しており、同じレイヤー数で他の手法と同等もしくはそれ以上の性能を上げていることが分かります。

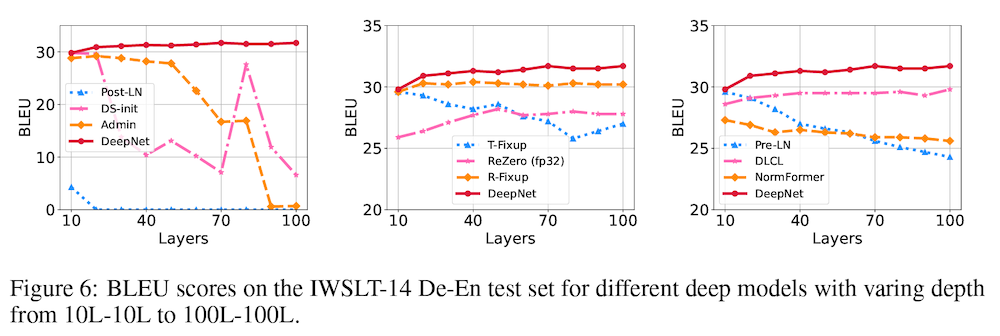
figure6

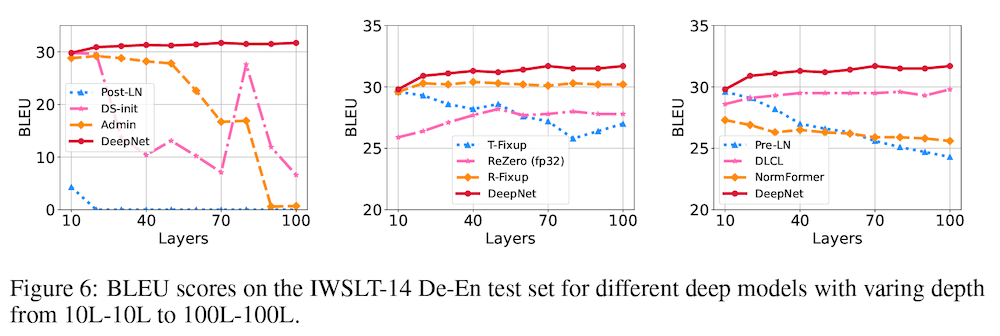
これは、レイヤー数に対して BLEU の値をプロットした上図 Figure 6 でも示されています。提案手法 (赤線) が、レイヤー数に関わらず、安定した訓練を実現し、良い性能を上げていることが分かります。

超多言語ニューラル機械翻訳による検証

論文ではまた、100言語をカバーした OPUS-100 コーパス (Zhang et al., 2020) を用いて、多言語ニューラル機械翻訳タスクにおいて、DeepNet モデルを検証しています。単一のモデルで複数の言語を翻訳する多言語ニューラル機械翻訳は、モデル容量への要求が高く、スケールが物を言いやすい典型的なタスクでもあります。

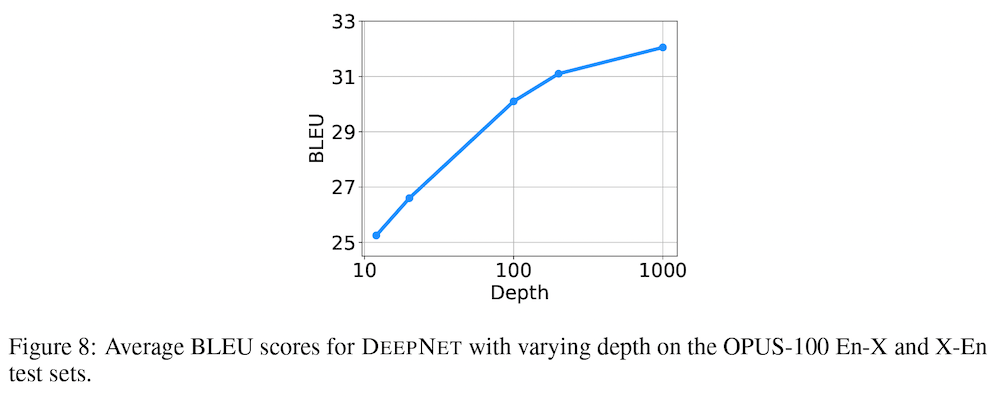
figure8

具体的には、1,000レイヤー (500レイヤーのエンコーダー＋500レイヤー) の DeepNet モデルを訓練しています。上図 Figure 8 に、レイヤーの数と性能の関係が示されていますが、1,000 レイヤーに達するまで、深さに対する対数の関係に従い、性能が安定して向上していることが分かります。なお、計算量の制限から、なんと 4 エポック分しか訓練していないということで、訓練時間をさらに伸ばすことによって、性能が向上する可能性がある、ということです。

最後に、DeepNet の限界を検証するために、訓練データに CCMatrix (Schwenk et al., 2019) などのデータを加えて 12B (120億) 個の対訳文までスケールさせ、100レイヤーのエンコーダー＋100レイヤーのデコーダーから成る DeepNet を訓練しています。

FLORES-101 (Goyal et al., 2021) を含む、複数の多言語翻訳ベンチマークを用いて評価したところ、これまでの SOTA (state-of-the-art; 最高性能) である M2M-100 (Fan et al., 2020, 以前の記事で解説済み) を大幅に上回る性能を上げたということです。これは、試した全ての評価データセットにおいて効果が見られ、データセットによっては、30% 以上も性能が向上したものもありました。

おわりに

本論文で提案された DeepNet、機械翻訳モデルで素晴らしい結果を残しており、これからの展開が楽しみです。

一方、理論的には、BERT などのエンコーダーのみのモデルや、GPT-3 などのデコーダーのみのモデルにも適用できるものですが、その検証実験が無いのが残念です。おそらく速報性を重視したためだと思われますが (arXiv のコメントにも、明確に "Work in progress" との記載があります)、今後、その他のタイプのモデルに対しても有効かどうかの検証が進むことが期待されます。最初に書いた通り、もし本論文で示された結果が他のタスクにも有効であるなら、機械学習のあらゆるタスクでトランスフォーマーが使われている現在において、そのインパクトは相当のものになる可能性があります。

なお、実装は、論文中からリンクがある UniLM ベースだと推測されますが、現段階でまだコードはコミットされていないようです。

関連記事

「とりあえずAdam」で本当に大丈夫？深層学習の最適化手法はこう選べ
深層学習モデルの訓練に欠かせない最適化手法（オプティマイザー）。多数の選択肢の中から適切な最適化手法をどう選ぶかについては、同僚やネット上から共有される経験則に頼っているのが現状です。本論文ではこの「最適化手法の選び方」を、体系的な実験に基づく証拠を元に調査し直し、有用なアドバイスを提供していますので、まとめて紹介したいと思います。
ステート・オブ・AI ガイド萩原 正人
最新研究から学ぶ 言語モデルの性能を向上させる5つの簡単なトリック
最近になって、言語モデルの性能を向上させる最新の研究が立て続けに発表されています。いずれも、比較的簡単な工夫で、トランスフォーマー・ベースの言語モデルの性能を改善したり、訓練を効率化したりといったことを可能にするものが多く、「GPT-3 超え」を達成したものもあれば、我々の日々の業務にも応用できそうなアイデアも多くあります。本記事では、最近の「言語モデルの性能向上テクニック」に関する文献をまとめて紹介します。
ステート・オブ・AI ガイド萩原 正人