1月の初めごろ、 DeepMind から DreamerV3 という強化学習アルゴリズムが発表されました。このアルゴリズムは、極めて難しいタスクとして知られる Minecraft のダイヤモンド収集タスクをゼロから解くことができたとして話題になりました。これは汎用的なアルゴリズムとしては初めての結果で特筆に値するものです。
そこで、本記事では DreamerV3 を提案した論文 "Mastering Diverse Domains through World Models (Hanfer et al., 2023)" について解説していきます。その際、その元になっている Dreamer (Hanfer et al., 2019)、DreamerV2 (Hanfer et al., 2020) などもおさらいしていきます。
文責:高木志郎
ステート・オブ・AI ガイドでは、人工知能・機械学習分野の最新動向についての高品質な記事を毎月5〜6本配信しています。購読などの詳細につきましては、こちらをご覧ください。また、Twitter アカウントの方でも情報を発信しています。
世界モデル
まずは Dreamer の基盤となる概念である世界モデルについて解説します。我々人間は、外界をシミュレーションをする内部モデルを脳内に形成していると考えられています。これによって外界からの刺激を予測しながら活動していると言われています。
同じように、強化学習環境のモデルをエージェントに獲得させることで、それをシミュレーターとしてエージェントに活用させよう、というのが世界モデルの発想です。強化学習はエージェントがある「状態」で「行動」をし、それによって得られた「報酬」をもとにより良い行動戦略(「方策」)を学習する枠組みです。強化学習における「環境」とは行動を受けて次の状態/観測と報酬を返すもののことを指します。世界モデルとはこの環境のモデルのことです。
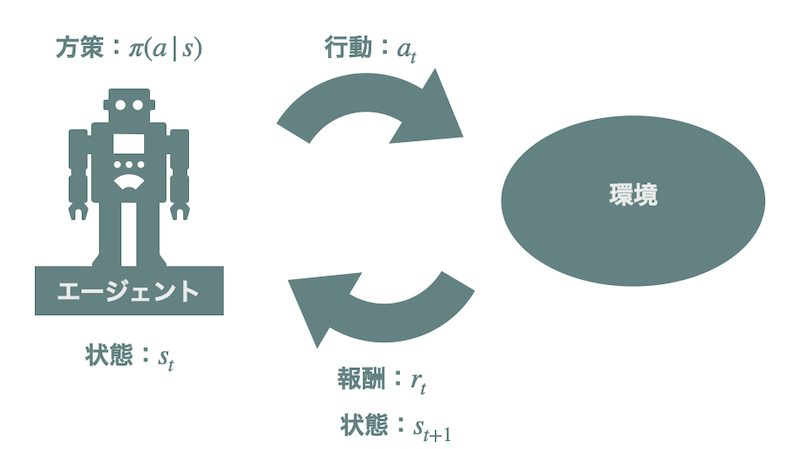
このような考えに基づいた研究は昔からありました。しかし、Ha らがこれらの研究の鍵となる概念を単純な枠組みに落とし込み「世界モデル」と呼び始めてから (Ha and Schmidhuber, 2018)、この呼称が一般に使われるようになったと考えられています。
世界モデルは、あるステップでの観測の低次元表現を構成する部分と、それまでのステップの情報を集約した表現を構成する部分からなります。前者には画像を観測として変分自己符号化器 (VAE) などが用いられます。また、後者には RNN (リカレント・ニューラルネットワーク) などが用いられます。以下の画像は (Ha and Schmidhuber, 2018) からの抜粋です。彼らは観測の表現を構成する部分を視覚モデル (Vision Model)、過去の情報の表現を構成する部分を記憶 RNN (Memory RNN) と呼んでいます。
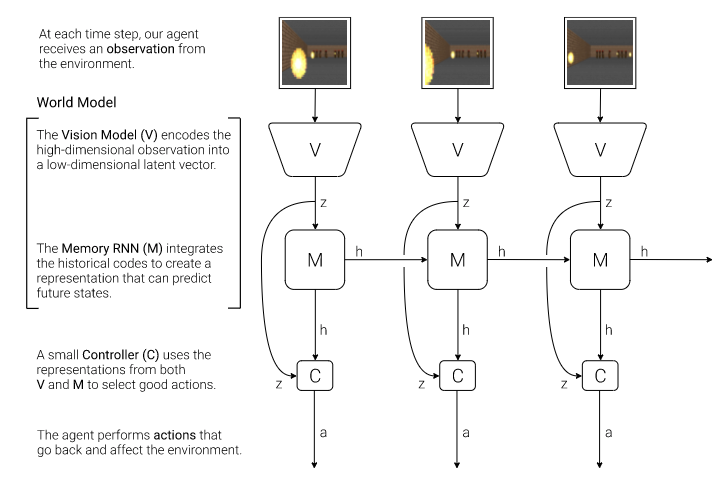
他の機械学習と同様、良い特徴表現を獲得することは強化学習でも重要です。その意味で強化学習において重要な環境の特徴表現を陽に学習する世界モデルベースの手法は重要です。また、一度優れた圧縮表現を獲得できればそれを環境のシミュレーターとして用いることもできます。そうすれば毎回実環境を用いることなく学習することもできるため行動学習の計算量を削減することができます。Dreamer もこの特徴を活用して効率的な行動学習を実現しています。
Dreamer
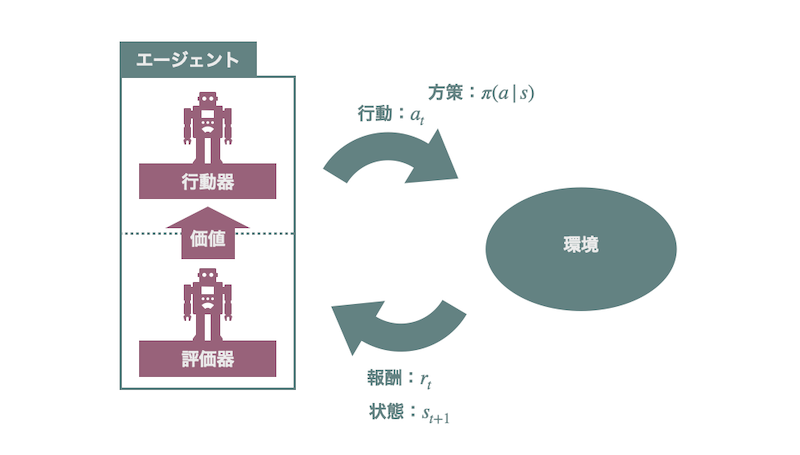
Dreamer は、前述した世界モデルと Actor-Critic 法を組み合わせた手法です。 Actor-Critic 法は強化学習の基本的な学習法の1つです。この手法では行動器と評価器と呼ばれる2つのモジュールを用意します。行動器は名前の通り行動を生成するモジュールです。最終的にはこの行動器が良い行動を出力できるように学習をします。
評価器は行動器の出力する行動の良さを判定するモジュールです。強化学習の目標は良い方策を獲得することです。そしてこの方策の良さはエージェントの行動や状態の価値と呼ばれる量などで推定されます。ですので、評価器はこの価値を推定するように学習します。この評価器が推定した価値にしたがって行動器が方策を更新していくのが、Actor-Critic 法です。
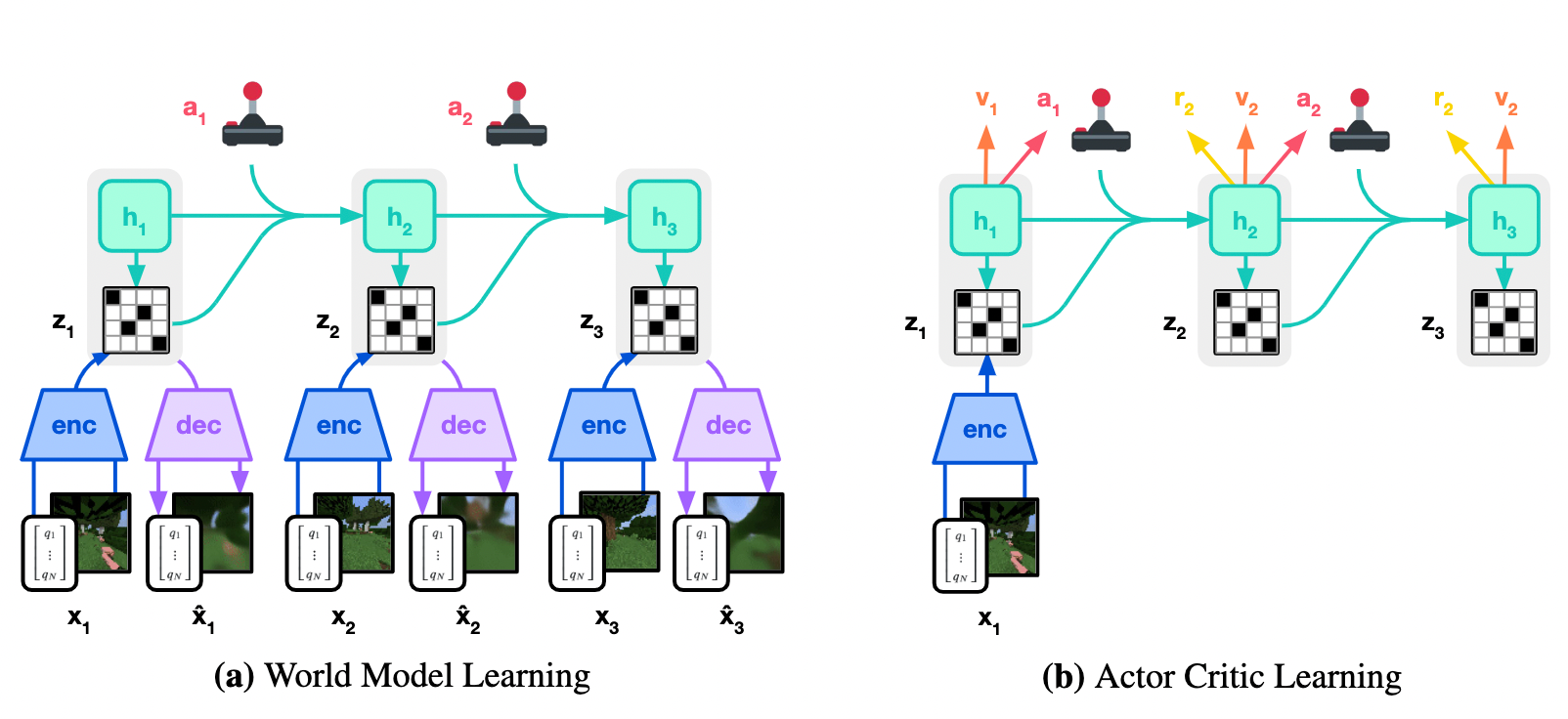
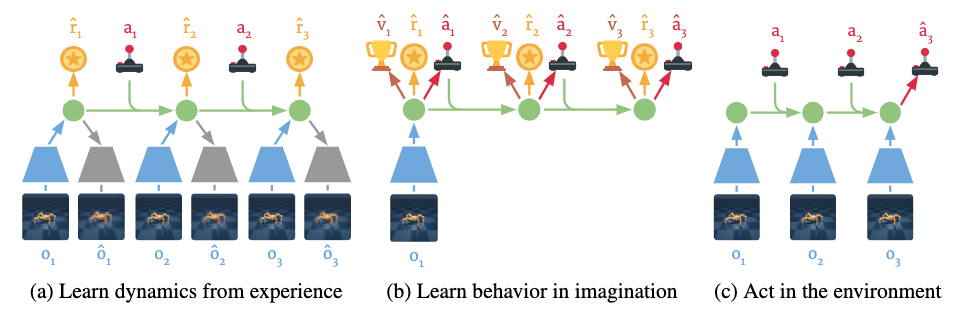
Dreamer ではまずエージェントを環境の中で動かして、世界モデルを学習させます (下図(a)) 。そして、学習された世界モデルを環境のシミュレーターとして用いて、この擬似環境の中で行動を学習させます (下図(b)) 。これを繰り返したのち、最後に、擬似環境で行動を学習したエージェントを実際の環境の中で動かすことで、タスクを解かせます (下図(c)) 。つまり、以下の 3 ステップで学習/評価をします。
- 世界モデルの学習 (下図(a))
- 行動の学習 (下図(b))
- タスクの実施 (下図(c))
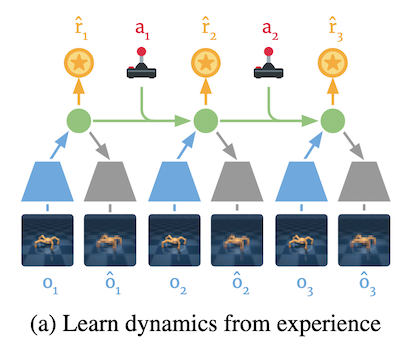
「1. 世界モデルの学習」では、強化学習の環境のモデルを学習します。上述したように強化学習において環境とは、エージェントの行動を受けて状態/観測と報酬の情報をエージェントに返し、今の状態を次の状態へ遷移させるものです。したがって、世界モデルとは、「状態」「報酬」「状態の遷移」のモデルに対応します。世界モデルの学習ではこれらを実際の環境から学習することを目指します。
「2. 行動の学習」では、学習した世界モデル、すなわち環境のシミュレータを使って、エージェントの行動を学習します。まず、観測の初期値を受け取った後、この観測をそのままエージェントには渡しません。代わりに、世界モデルがそこから状態の予測を出力し、それをエージェントに渡します。エージェントはその状態を受け取り、それに対して行動を返します。これを受けて世界モデルは報酬の予測値を計算し、これをエージェントに返します。エージェントはこの予測報酬をもとに、自分の行動を改善します。そして最後に、世界モデルが次の状態を予測し、状態を更新します。
これ以降は実際の環境からの観測は受け取らずに、全て世界モデルが計算した状態のみで学習をしていきます。これはある意味でエージェントが現実世界ではない「夢の中」で学習しているということができるかもしれません。これが、本手法が Dreamer と名付けられた理由だと考えられます。
このように、世界モデルを学習することで実際の環境でエージェントを動かさずに行動を学習することができます。これによって一度の行動学習に必要な計算量を低く抑えることができます。そのお陰で例えば相対的に多くの行動学習を並列的に実行することができます。これが世界モデルを陽に学習する Dreamer の強みの一つです。
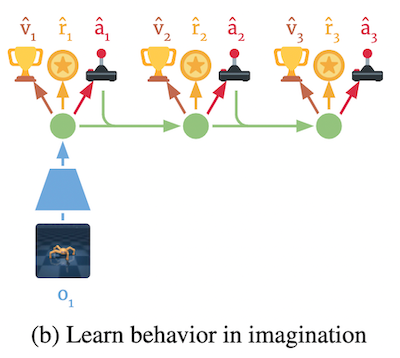
「3. タスクの実施」では、獲得した世界モデルと行動戦略を使って、実際の世界と相互作用することで、タスクを解かせます。以上が Dreamer の概要です。次からは「1. 世界モデルの学習」と「2. 行動の学習」についてより詳しく説明していきます。
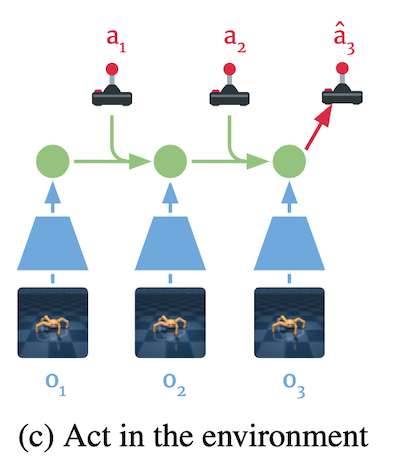
Dreamer における世界モデルの学習
Dreamer の論文では潜在状態の学習法として複数手法が検討されていました。その中でも Recurrent State Space Model (RSSM) というモデルを用いて潜在状態をモデル化した方法が DreamerV2 以降のベースになっています。ですので、本記事ではこちらについてのみ紹介します。これは Dreamer の筆頭著者である Hafner らが 2018 年に提案した Deep Planning Network (PlaNet) というエージェントで用いられていたものです (Hafner et al., 2018) 。
RSSM は、潜在状態を決定論的な潜在状態 $h$ と確率的な潜在状態 $z$ に分けて表現する、潜在状態のモデルです。これは、3つの構成要素からなります。1つ目が系列モデル (Sequence model) $f_{\phi}$ です。これは過去から現在ステップ $t$ までの情報をモデル化します。2つ目が符号化器 (Encoder) $q_{\phi}$ です。これは系列モデルの潜在表現 $h_t$ と現在の観測 $x_t$ から確率的な表現 $z_t$ を生成します。3つ目が環境変動予測器 (Dynamics predictor) $p_{\phi}$ です。これは系列モデルの潜在表現のみから表現を生成します。ただし、 $a_{t-1}$ はステップ $t-1$ での行動で、 $\phi$ はネットワークのパラメータ全部をあわせたパラメータベクトルです。
$$
\text { RSSM } \begin{cases}\text { Sequence model: } & h_t=f_\phi\left(h_{t-1}, z_{t-1}, a_{t-1}\right) \\
\text { Encoder: } & z_t \sim q_\phi\left(z_t \mid h_t, x_t\right) \\
\text { Dynamics predictor: } & \hat{z}_t \sim p_\phi\left(\hat{z}_t \mid h_t\right)\end{cases}
$$
下図は RSSM モデルの全体図を表したものです。
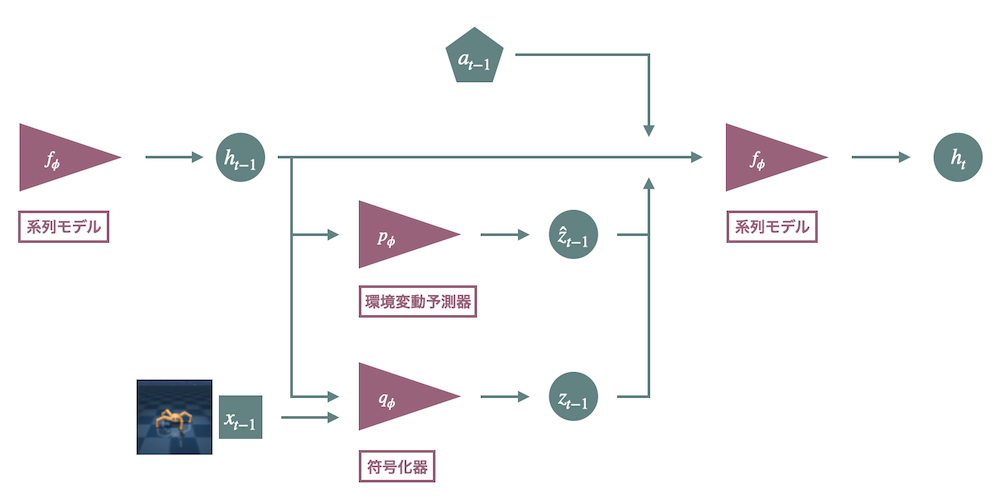
環境のモデルを学習したのち、系列モデルと環境変動予測器を環境のシミュレーターとして用います。これにより、画像などの高次元の観測情報を保持することなく、行動の学習が可能になります。なお、それぞれの構成要素の呼称には Dreamer から DreamerV3 にかけて揺らぎがありますが、ここでは DreamerV3 の呼称を採用しています。
このモデルの表現 ($z_t$、 $\hat{z}_t$、 $h_t$) がどのような表現を獲得するかはどのような目的関数を最適化するように学習するかに依存します。 Hafner らはこの学習のために、2つの予測器を導入しました。1つ目が復号化器 (Decoder) です。これは潜在表現から観測を再構成します。2つ目が報酬予測器 (Reward predictor) です。これは文字通り報酬を予測します。そして、これらの対数損失が最大になるような表現を獲得させるようにアルゴリズムを設計しています。
$$
\text{Decoder}: \quad \hat{x}_t \sim p_\phi\left(\hat{x}_t \mid h_t, z_t\right)\\
\text{Reward predictor}: \quad \hat{r}_t \sim p_\phi\left(\hat{r}_t \mid h_t, z_t\right)
$$
下図は、前掲の世界モデルの説明図において予測器がどこに該当するかを示した図です。
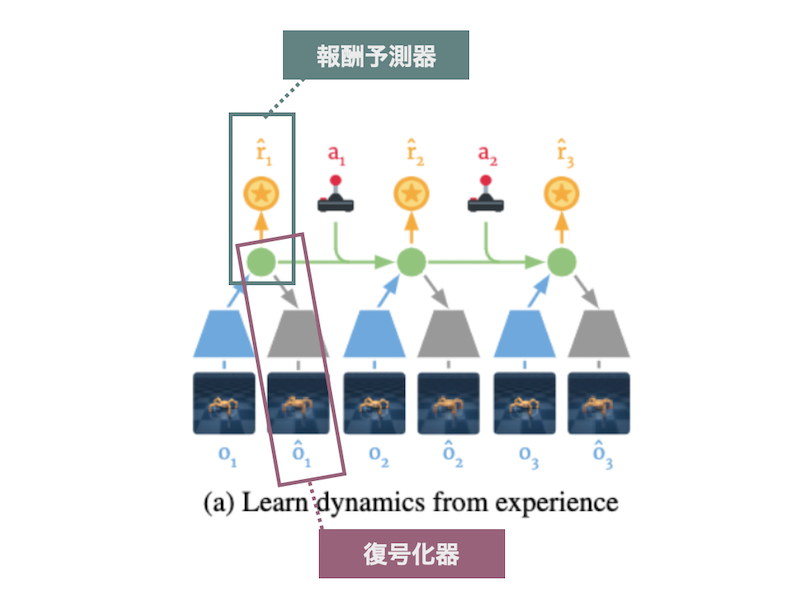
Dreamer における世界モデルは、潜在表現を符号化する RSSM とその潜在表現を用いて予測をするこれらの予測器から構成されます。
前述したように、行動学習時には観測を埋め込む符号化器は用いられません。代わりに、環境変動予測器がシミュレータとして用いられます。したがって、観測を入力に受けなくても環境変動予測器が符号化器の出力にある程度似た表現を出力する必要があります。
そこで、前述した予測学習に加えて、正則化項を加えます。具体的には、符号化器の出力 $z_t$ と環境変動予測器の出力 $\hat{z}_t$ が離れすぎないように、 KL ダイバージェンスで正則化をします。
これまで述べた予測器の学習と直前で述べた正則化を一つの損失にまとめたのが全体の損失です。Dreamer ではこれらを一斉に学習します。具体的には、世界モデルを学習するために最小化する損失 $\mathcal{L}(\phi)$ は次のようになります。
$$
\mathcal{L}(\phi) \doteq \mathrm{E}_{q_\phi}\left[\sum_{t=1}^T\left(\mathcal{L}_{\text {pred }}(\phi) +\beta \mathrm{KL}\left[q_\phi\left(z_t \mid h_t, x_t\right) | p_\phi\left(z_t \mid h_t\right)\right] \right)\right]
$$
ただし、 $T$ はステップ数で、 $\mathcal{L}_{\text {pred }}(\phi)$ は予測器についての損失の和です。
$$
\mathcal{L}_{\text {pred }}(\phi) \doteq-\ln p_\phi\left(x_t \mid z_t, h_t\right)-\ln p_\phi\left(r_t \mid z_t, h_t\right)
$$
Dreamer における行動の学習
Dreamer シリーズでは、 Actor-Critic 法を用いて行動を学習します。 Actor-Critic 法では、2つのモジュールを用意します。
1つ目が行動器 (Actor) $\pi_\theta$ です。これはある状態のもとで行動を生成します。2つ目が、評価器 (Critic) $v_\psi$ です。これはあるエージェントの行動の良さを評価します。ここではエージェントが到達した状態の良さである状態価値から行動の良さを評価します。
$$
\text{Actor}: \quad a_t \sim \pi_\theta\left(a_t \mid s_t\right)\\
\text{Critic}: \quad v_\psi\left(s_t\right) \approx \mathrm{E}_{p_\phi, \pi_\theta}\left[R_t\right]
$$
ただし、 $s_t = (h_t,z_t)$ は決定論的潜在状態と確率的潜在状態を合わせた状態です。また、 $R_t \doteq \sum_{\tau=0}^{\infty} \gamma^\tau r_{t+\tau}$ はあるステップ $t$ 以降の割引報酬の和です。これを収益と呼びます。
評価器は状態価値を予測するように学習します。一方行動器は評価器が予測した状態価値を最大化する行動を出力するように学習をします。この時、評価器が目指す状態価値の推定値として、DT(λ) 法で用いられる λ 収益 $R_t^{\lambda}$ を用いています。
$$
R_t^\lambda \doteq r_t+\gamma_t \begin{cases}(1-\lambda) v_{\psi}\left(s_{t+1}\right)+\lambda R_{t+1}^\lambda & \text { if } t<T, \\ v_{\psi}\left(s_T\right) & \text { if } t=T\end{cases}
$$
これは直観的には重みづけられた収益の和です。この重みは異なる最大ステップ数における、最大ステップ数に応じて決まります。詳細については他の強化学習の教科書を参照してください。この λ 収益を用いて、行動器と評価器はそれぞれ以下の損失を最小化するように学習します。
$$
\mathcal{L}_{\text {actor}}(\theta) \doteq - \mathrm{E}_{\pi_\theta, p_\phi}\left[\sum_{t=1}^{T - 1} \mathrm{R}^\lambda_t \right], \ \
\mathcal{L}_{\text {critic}}(\psi) \doteq \mathrm{E}_{\pi_\theta, p_\phi}\left[\sum_{t=1}^{T - 1} \frac{1}{2} \left(v_{\psi}\left(s_{t}\right) - \mathrm{R}^\lambda_t\right) \right] \
$$
DreamerV2
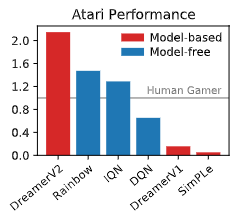
DreamerV2 は、世界モデルとしては初めて Atari ベンチマークタスクで人間に匹敵する性能を発揮しました。また、単一 GPU の手法の中では初めて、モデルベースの手法としてモデルフリーの手法を上回る性能を見せました。
下の図がそれを表したグラフです。縦軸は Atari における正規化されたスコアの中央値を表しています。長らくトップを走っていた Rainbow (Hessel et al., 2017) などのモデルフリーの手法を上回るスコアを叩き出していることがわかります。このような結果から DreamerV2 は大きな注目を集めました。
この DreamerV2 はほぼ Dreamer を踏襲しています。したがって本記事では主要な変更点に注目して紹介していきます。
DreamerV2 の主な変更点は 1. 潜在変数へのカテゴリ変数の利用、と 2. KL 平衡 (KL balancing) の導入です。これらはそれぞれ世界モデルの学習における変更点になっています。そこで、まずは世界モデルでの変更点について説明していきます。
DreamerV2 における世界モデルの学習
1. 確率的潜在状態の離散化
DreamerV2 の主な変更点の一つが、確率的潜在状態の離散化です。前節では説明しませんでしたが、Dreamer では確率的潜在状態をサンプリングする潜在変数をガウスにしていました。具体的には分散共分散行列が対角行列となる多変量正規分布に従う確率変数を用いていました。DreamerV2 ではこれを離散変数に変更しています。
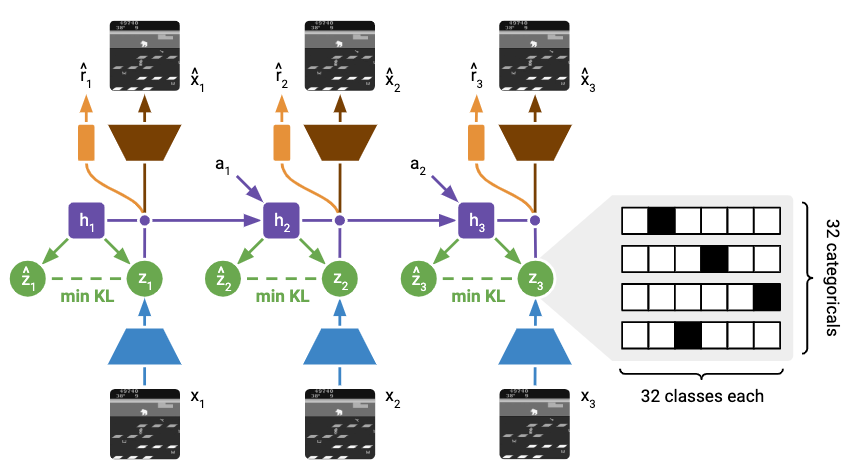
具体的には、32本のカテゴリ変数ベクトルを用意します。各ベクトルの次元も32で、それぞれの一つの次元が一つのクラスに対応します。モデルは、 1. 各カテゴリ変数ベクトルが何を表現するのか、 2. 各ベクトルのクラスがそれぞれ何を意味するのか、を学習します。
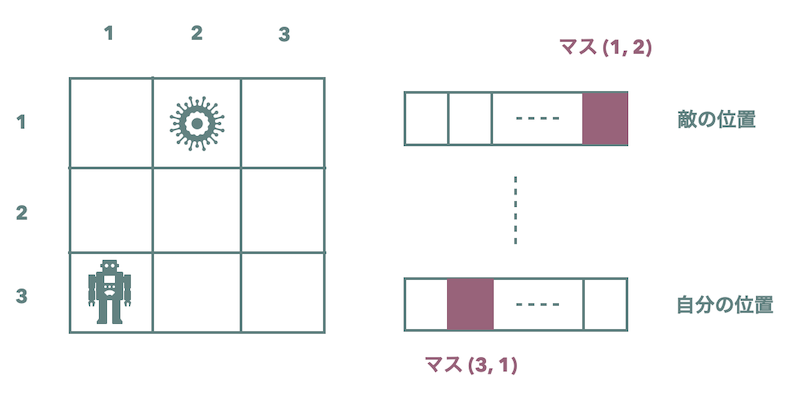
例えば、あるベクトルはプレイヤーがどこのマスにいるかを表し、各クラスはマスの番号に対応しているかもしれません。また、別のベクトルは、相手がどのマスにいるかを表すかもしれません。下図は離散変数で状態を表現したときのイメージ図です。このような離散ベクトの組み合わせで状態を表現するのが DreamerV2 です。
このような離散化が性能改善に繋がった理由として、「ガウスではうまくできない複数のありうる観測の状態を表現できたからではないか」と著者たちは述べています。 Google の公式ブログから抜粋した次の図をもとにその直観を説明します。
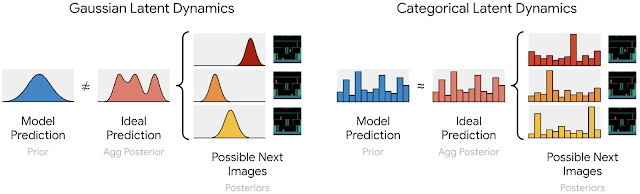
Atari のゲームでは、同じ状態からあり得る状態の遷移先が複数存在する場合があります。その場合、状態を分布で表現しようとしたら、多峰性の分布で表現できるのが理想です。しかしガウス分布は単峰性の分布であるため、このような分布をうまく表現することができません (上図左) 。
一方で離散分布であれば、足し合わせればそれぞれのありうる状態のところにピークが立ってくれます (上図右)。これによって次の状態をよりよく表現できたことが性能改善につながったのではないかと著者たちは推察しています。
2. KL 平衡の導入
二つ目の主な変更点が、KL 平衡 の導入です。世界モデルの損失では環境変動予測器の出力が符号化器の出力に近づくように KL ダイバージェンスによる正則化を加えていました。これによって観測の情報がなくとも観測を再構成できるだけの情報を環境変動予測器が獲得することができました。
一方 KL を最小化すると符号化器の出力も環境変動予測器の出力に近づきます。これによって訓練時の観測に過適合せずに汎用性の高い表現を獲得できるようになるという正則化のような働きもしています。
しかし、環境変動予測器が十分な表現を獲得できていない時に、符号化器をそれに近づいていくのは問題を引き起こします。そこで、そこで著者らは KL の項を2つの項に分離しました。1つめが環境変動予測器の出力を符号化器の出力に近づける項です。2つめがその逆です。
そして、前者の係数 $\alpha$ を後者の係数 $1 - \alpha$ よりも大きく取るようにしました。これによって環境変動予測器のほうが早く学習が進み、前述の問題に対応できるようになります。具体的には、前述の KL 項を以下のように変更しています。

ただし、 approx_posterior が符号化器、 prior が環境変動予測器に対応しています。 stop_grad は勾配を流さない処理で、 compute_kl が KL ダイバージェンスを計算する処理です。
DreamerV2 における行動の学習
次に行動学習における変更点を説明します。前述したように DreamerV2 での主な変更点は世界モデルについての修正です。行動学習においては学習をうまくいかせるための細かい修正が加えられています。評価器の主な変更点は、学習対象であるλ収益について勾配を流さないようになったことぐらいです。
行動器の変更点としては、探索を促すためのエントロピー項が追加されました。これは、Atari の学習では環境内の探索が不可欠であるためです。
また、 Dreamer の論文では行動空間が連続でしたが、 Atrai は行動空間が離散的です。著者らによると Atari 環境では前回導入した損失では学習がうまくいかなかったようです。そこで、離散行動空間の場合は REINFORCE 損失を用いることを新たに提案しています。
DreamerV3
いよいよ DreamerV3 についての説明に入ります。まず最初に Dreamer V3 の主な結果について説明したいと思います。DreamerV3 の結果で押さえておくポイントは以下の3つだと考えます。
- 規模が大きいモデルだと性能が上がる上、サンプル効率も良くなることを示したこと
- 様々なテクニックを駆使することにより、様々な環境で必要最小限のハイパーパラメータ調整などで良い性能をだしたこと
- 汎用的な世界モデルベースの手法として初めて Minecraft のダイヤモンド収集タスクを解けたこと
ですので、これらの結果についてそれぞれ説明していきたいと思います。
1. モデルの大きさの影響
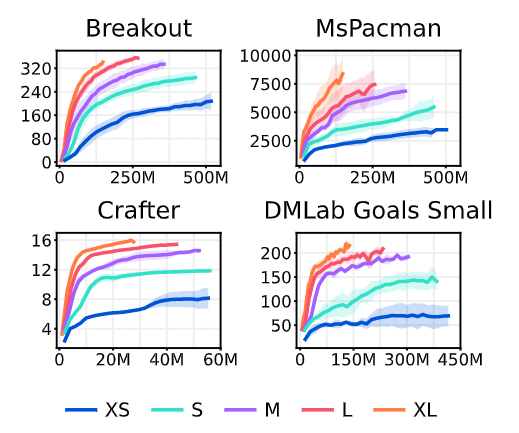
まず一つ目のモデルの大きさの影響について説明します。下の図はモデルのパラメータ数を 800 万から 2 億まで増加させた時の異なるタスクにおける性能の変化です。横軸がステップ数、縦軸がスコアで、 XS から XL になるにかけてモデルが大きくなります。
この図を見ると、モデルを大きくすると最終的な性能が上がることがわかります。それだけでなく、より少ないステップ数で高いスコアにたどり着いていることがわかります。すなわち、モデルのサイズが増えることで最終的な性能が上がるだけでなくサンプル効率が上がっていることもわかります。これは今後の研究の方向性にも示唆を与える結果なのではないかと思います。
2. さまざまな環境への適応
DreamerV2 では、 Atari のタスクを解けるように Dreamer に改良が施されました。 DreamerV3 の目的は、できるだけ汎用的な設定で複数のタスクを達成できるようにすることです。したがって、出来るだけ各環境やタスクに特化したヒューリスティクスやハイパーパラメータの調整をせずに、性能を発揮するための工夫がされています。具体的には、環境ごとの変動に頑健になるような工夫が色々と導入されています。
この点に注意しながら、 まずは DreamerV3 で導入された工夫について紹介していきます。そしてその後でこれらの工夫が施された DreamerV3 の各ベンチマークでの性能についてみていきいます。細かい工夫が多いので、ここでは主要な工夫についてのみ取り上げます。ここで取り上げなかったものについては論文を参照してください。
Symlog 予測の導入
報酬や状態価値は環境やタスク毎に定まります。したがって、その値の大きさはそれぞれの環境によって大きく変化し得ます。そのため、複数のタスクに適応するためにはこれらの変動に対して頑健でなければなりません。そこで著者たちは「symlog」という関数を導入して値を正規化することを提案しています。値が正規化されれば、環境変動による影響を少なくすることができます。
symlog 関数とその逆変換である symexp 関数は次のように定義される関数です。
$$
\text{symlog}(x) \doteq \text{sign}(x)\ln(|x|+1) \ \ \
\text{symexp}(x) \doteq \text{sign}(x)(\exp(|x|)-1)
$$
この symlog 関数は、入力 $x$ を負の値の場合も含めて対数スケールに変換します。下の図は symlog の出力を示したものです。入力の値が小さいところでは恒等関数の出力のような値になっています。また、値が大きくなると正と負の値それぞれで log 関数の出力のような値になっていることがわかります。
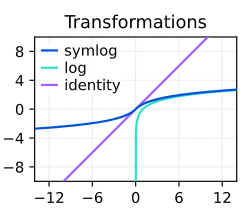
著者たちはこの symlog 関数を復号化器、報酬予測器、評価器のそれぞれが予測する「対象に」対して適用しました。各予測器は、変換された値をこれらの値を予測するように学習します。例として、予測器を $f(x, \theta)$ 、予測対象を $y$ としてその二乗誤差 $\mathcal{L}(\theta)$ を最小化する場合を考えます。この場合は、以下のようにして予測値 $\hat{y}$ を計算するイメージです。
$$
\mathcal{L}(\theta) \doteq \frac{1}{2}\left( f(x, \theta) - \text{symlog}(y)\right)^2 \
\hat{y} \doteq \text{symexp}\left( f(x, \theta) \right)
$$
DreamerV3 における世界モデルの学習
DreamerV2 で KL 項を分離しました。しかし、依然として符号化器が入力の情報を使わずに環境変動を予測できるような表現を学習してしまう恐れがあります。特に、観測のうちどの部分が重要な情報かは環境によって大きく異なります。したがって、環境毎にハイパーパラメータを調節せずに済む方法でこの問題に対処する必要があります。
そこで著者たちは自由ビット (Free bits) という方法を使いました。これは、潜在変数が獲得する情報量の最小値について制約を加えるという手法です。 (Kingma et. al 2016) で導入されました。
具体的には、前述した分割された KL 項それぞれについて、値が 1 以上であればそのまま KL 項を計算し、 1 以下であれば 1 を返すように修正します。これによって、 KL 項の大きさが 1 以上の時のみ、 KL 項が学習に影響を与えるようになります。この工夫によって環境毎に正則化の強さを変えることなく複数環境に適応できるエージェントが学習できたと著者たちは述べています。
DreamerV3 の行動の学習
DreamerV2 までは、評価器の損失は λ 収益との間の二乗誤差でした。しかし今回の設定ではばらつきの大きい収益の期待値を予測しなければなりません。そのような状況ではこの方法だと学習が遅くなってしまうと著者たちは述べています。
そこで著者たちは、連続値である収益たちを twohot ベクトルで離散的に表現しました。そしてそれに対して分類問題を解かせるようにしました。これは Muzero などでも用いられていたテクニックです (Schrittwieser et. al 2019) 。
連続値を離散化するための区間を $B = [b_1, ..., b_{|B|}]$ とすると、 twohot ベクトルへは次のように変換します。
$$
\text { twohot }(x)_i \doteq \begin{cases}
|b_{k+1} - x| / |b_{k+1} - b_{k}| & \ \ \text{if} \ \ i = k \\
|b_{k} - x| / |b_{k+1} - b_{k}| & \ \ \text{if} \ \ i = k + 1 \\
0 & \ \ \text{else}
\end{cases} \ \ \ \ \ \ k \doteq \sum_{j=1}^{|B|} \delta(b_j < x)
$$
例えば、 $B = [-2, -1, 0, 1, 2]$ で、 $x=1.3$ とします。この時、 $k = 4$、$|b_{k+1} - x| / |b_{k+1} - b_{k}| = |2 - 1.3|/|2 - 1| = 0.7$ 、 $|b_{k} - x| / |b_{k+1} - b_{k}| = |1 - 1.3|/|2 - 1| = 0.3$ となります。
したがって、 $\text{twohot}(x) = [0, 0, 0, 0.7, 0.3]$ となります。つまりこれは、 1.3 という連続値を「$B$ という区間の四番目の離散値に 0.7、五番目の離散値に 0.3 の重みのある値」として表現していることを意味します。
著者たちは、 λ 収益を symlog 変換した後に twohot 変換したものである $y = \text{sg}(\text{twohot}(\text{symlog}(R_t^{\lambda})))$ を学習対象としました。そして、評価器にソフトマックス交差エントロピー損失を最小化するように学習をさせました。この離散化は報酬予測の時にも用いたと著者たちは述べています。
行動器については、行動器の損失の λ 収益を $\max(1, S)$ で割って正規化することを提案しています。ただし、 $S$ は λ 収益たちの 95 パーセンタイルと 5 パーセンタイルの値の差を用いています。
これによって、報酬が疎な場合も密な場合も同様のエントロピー項の係数を使って学習をすることができたと著者たちは主張しています。著者らが用いたタスクには、簡単なエピソードによってもたらされる外れ値的に大きな収益があるようなタスクがあったそうです。この手法は、このようなタスクに対して外れ値に対して頑健な学習を可能にしたと報告されています。
複数ベンチマークでの性能評価
ここから、 DreamerV3 の評価実験の結果を説明します。著者たちは DreamerV3 が複数の環境に適応できるかを確かめました。そのために、複数のベンチマークタスクでその性能を評価しました。これは行動空間が離散/連続なもの、空間が 2D/3D なもの、報酬が疎/密なものまで様々な環境から構成されています。
具体的には、次のベンチマークについて同じハイパーパラメータで学習及び評価をしました: Proprio Control Suite (Tassa et al., 2018)、Visual Control Suite (Tassa et al., 2018)、Atari 100k (Kaiser et al., 2019)、Atari 200M (Bellmare et al., 2013)、BSuite (Osband et al., 2019)、Crafter (Hanfer 2018)、DMLab (Beattie et al., 2016)。
下の図が DMLab 以外の各ベンチマークでのスコアの比較です。青色が提案手法で、それ以外がそれぞれのタスクに特化してハイパーパラメータを選んで調整された手法です。この結果から、提案法はこれら既存手法と同等ないしそれ以上の性能を発揮していることがわかります。ここのベンチマークの詳細については論文を参照してください。
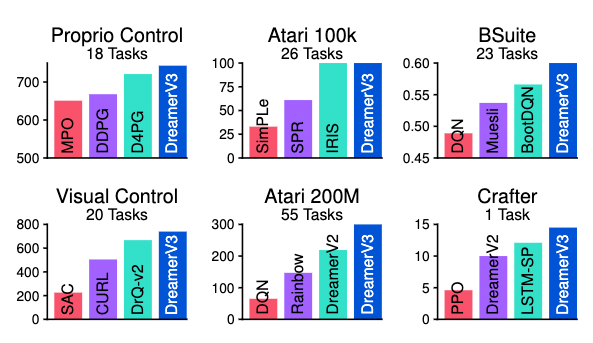
著者たちは今回導入した工夫がどれだけ学習に寄与したかも調べています。具体的には上で説明したような「世界モデル」や「評価器」への工夫の影響について個別に調べています。報告されているのは前述のベンチマークタスクのいくつかに対しての結果です。
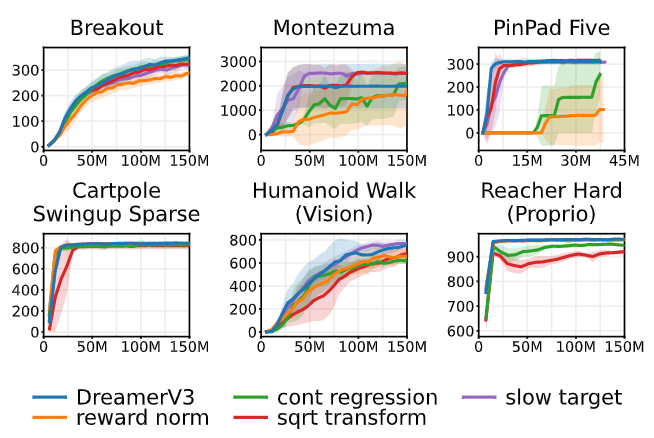
まずは、世界モデルへの変更の影響を見てみます。下の図が実験結果です。横軸がステップ数、縦軸がスコアで、青い線が提案手法を表しています。緑色が自由ビットを用いなかったもの、オレンジが KL 平衡をしなかったもの、赤色が symlog 変換をしなかったものです。これを見ると、タスク全体で見た時にはこれらのいずれの手法も学習に寄与していることがわかります。
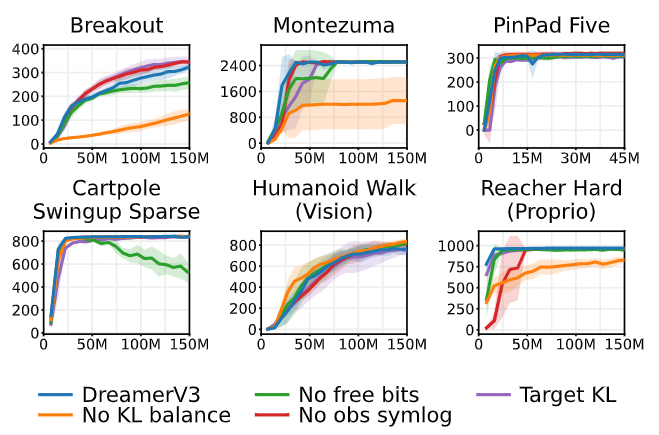
次に、下の図が評価器への変更の影響を調べた結果です。この中で緑色の線の「const regression」が twohot 変換による分類をしなかったものです。この結果を見ると、特に Montezuma や PinPad Five などで性能が劣化していることがわかります。すなわち、twohot 変換はこれらのタスクを解くためには重要であったことがわかります。
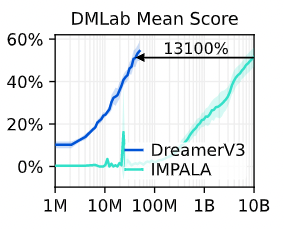
最後に、DMLab についての結果を紹介します。下図がその結果で、横軸がステップ数、縦軸が平均スコアです。青色が提案手法で、水色が比較対象です。この図を見ると、提案手法は既存手法よりも早く高いスコアに到達していることがわかります。すなわち、既存手法に比べてサンプル効率を改善していると言えます。
Minecraft ダイヤモンド収集タスク
この論文の大きな成果の一つが、汎用的な手法として初めて Minecraft のダイヤモンド収集タスクを解くことができたことです。このタスクはダイヤモンドを取得するまでに他のアイテムも取得しなければならない難しいタスクです。これまでもこのタスクを解くことができる手法があったものの、それらはタスクに対してハイパーパラメータなどを細く調整していたそうです。
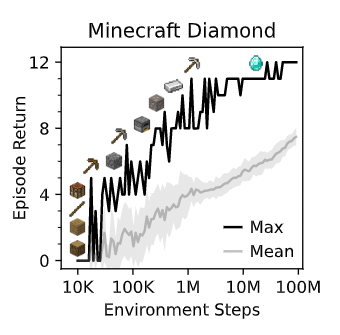
これに対して、著者たちは他のタスク同様ハイパーパラメータを特別に調整することなく提案手法を学習/評価しました。その結果が以下の図です。縦軸が収益で、横軸がステップ数です。
この図を見ると、ステップ数を重ねるごとに収益がちゃんと増えていっていることがわかります。また、ここで表示されている画像は中間アイテムを表しています。論文中で著者たちはエージェントが学習を重ねる毎にちゃんと中間アイテムを収集し、タスクを達成できたことを報告しています。
終わりに
この記事では、DreamerV3 とそれに至るまでの Dreamer、 DreamerV2 について紹介してきました。 DreamerV3 自体は以前の Dreamer シリーズからアルゴリズムなどの面では大きな変化がなく研究としてはあまり面白くはないかもしれません。言ってしまえば「モデルを大きくして細かい工夫を追加したら良い結果が出た」という類のものなのでそれまでといえばそれまでです。
難しい問題は、綺麗なアイデアのみで本当に解けることは少なく、泥臭い工夫が重要になることが多いと個人的には思っています。そういった細かい工夫は、研究としては「新規性がない」と言われることもありますが、それらを共有することは、実際に問題を解こうと試みている人たちにとっては重要な知見です。
その意味で、今回取り上げた DreamerV3 のような論文は個人的には好感を持てます。また、世界モデルベースの手法が、単純な工夫でハイパラの細かい調整もなくダイヤモンド収集タスクを解くことができたということ自体は示唆深い結果だと思います。今後、この研究の成果を受けて世界モデルベースの研究がより一層注目されていくかもしれません。
関連記事