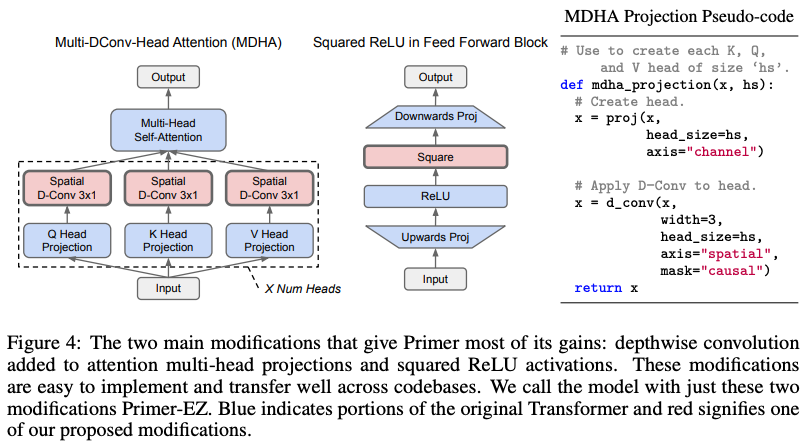
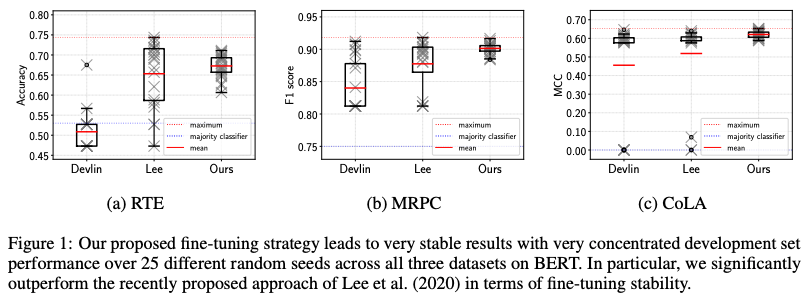
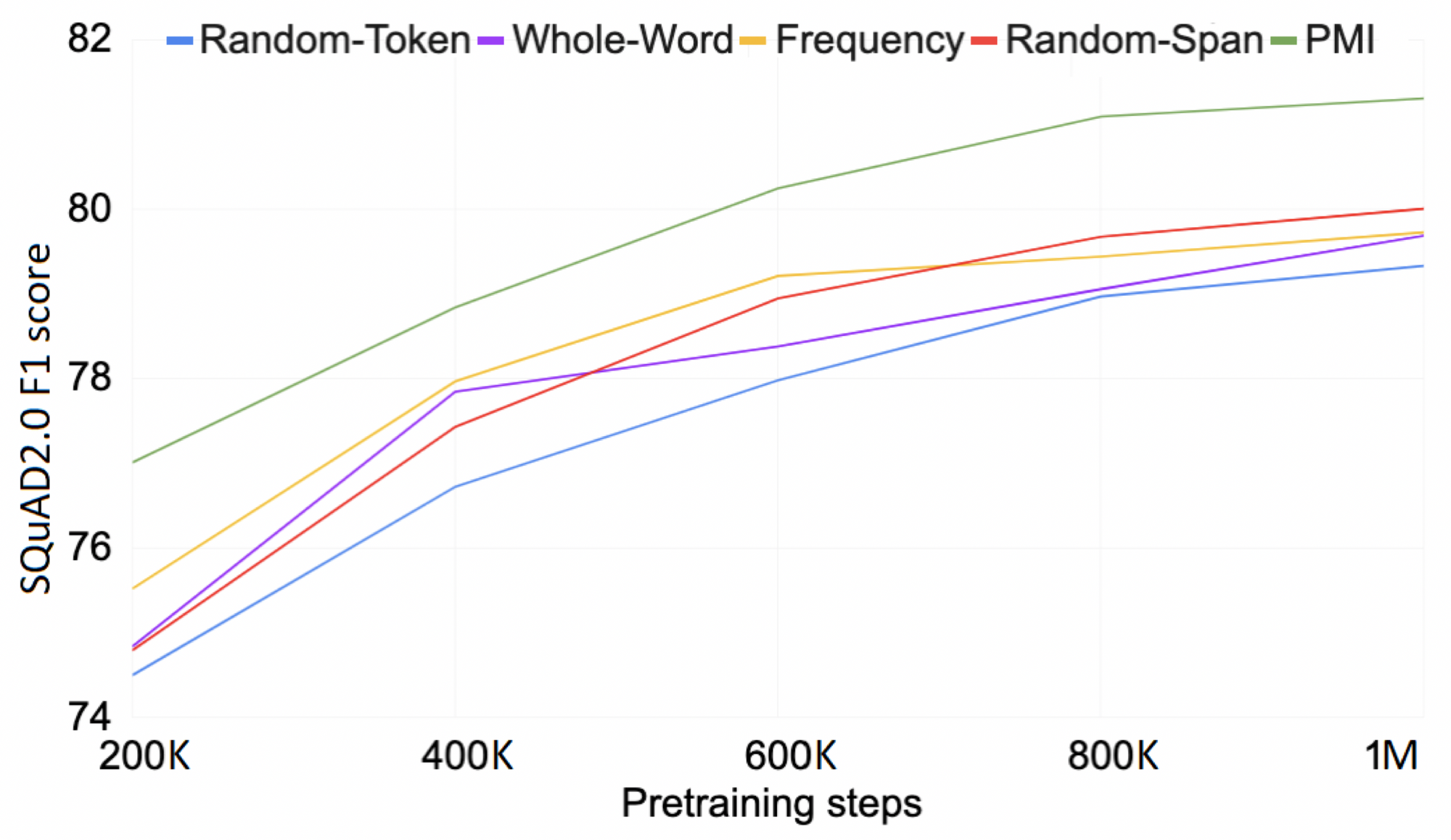
BERT や RoBERTa といったマスク言語モデルは、一部を黒塗りしたテキストを復元するという練習問題を何億問も解くことで汎用のテキストエンコーダに成長します。ところが練習問題の中には「内閣■■大臣は…」のように文全体を見なくても解けてしまう簡単なものがたくさん含まれています。今回紹介する ICLR 2021 の論文 “PMI-Masking: Principled masking of correlated spans” では、これらの簡単すぎる問題を難しい問題に差し替えて BERT を「甘やかす」のをやめると言語モデルの品質が向上する… という面白い話が示されています。当該論文を理解するための前提知識の説明からじっくり1本ご紹介します。

文責：横井祥（東北大学）

ステート・オブ・AI ガイドでは、人工知能・機械学習分野の最新動向についての高品質な記事を毎月5〜6本配信しています。購読などの詳細につきましては、こちらをご覧ください。また、Twitter アカウントの方でも情報を発信しています。

文献情報・参考 URL

まとめ

  • 共起しやすいトークン列（連語・複単語表現）をマスク言語モデルの事前訓練時にまとめてマスクすることで、訓練の効率も後段タスクの性能も向上。
  • 3トークン以上からなる連語の同定のために自己相互情報量を拡張。
  • マスク言語モデルの事前訓練戦略と後段タスクに必要な表現学習の間にギャップが存在することを示唆。

これは自然言語処理に詳しいかた向けの要約です。このあと前提知識から丁寧に説明します。

背景

本論文を理解するために必要なふたつの背景知識について簡単に説明します。

マスク言語モデル

大規模な生コーパスで汎用モデルを事前訓練し、その後少量のラベルつきデータでパラメータを微調整（fine-tuning）すれば良い。現代の自然言語処理の基本的なパラダイムのひとつです。

生コーパス、つまり人手によるタグ付けが行われていないただのテキストを用いるのは重要なポイントです。データセット作りやアノテーションという作業コストを回避でき、結果として巨大なコーパスを用いてモデルを訓練することできるからです。事前訓練用のコーパスのサイズを大きくすればするほど良いモデルができあがるという知見は、最近ではスケーリング則（scaling law）という標語のもとに経験的・理論的検証が積極的に進められています（Kaplan et al., arXiv 2020）。

汎用モデルの事前訓練にはいくつかのやり方がありますが、BERT（Devlin et al., NAACL 2019）や RoBERTa（Liu et al., arXiv 2019）が採用している マスク言語モデル（masked language models）は特に注目されている方法のひとつです。その名前の通り一部をマスク（黒塗り）したテキストを復元するというタスクがモデルに課されます。

たとえば、モデルは「鹿児島県は■■の名産地で加工品としては酸味が特徴のジュースが人気」のように一部をマスクしたテキストを受け取り、マスク部（■■）にどんな単語が入っていたかを予測します。この形式の練習問題は、見ての通り生コーパスから自動的にいくらでも作ることができるのが良いところです。

皆さんはこの穴埋め問題を解けそうですか？日本語の理解という超高等技能を備えた言語計算機……つまり脳を持つ我々は、周辺文脈をみるだけで「少なくとも果物の名前が入りそうだな…」と予測できますね。BERT や RoBERTa はこのような練習問題を何億問も解くことで強力な言語エンコーダに成長していきます。

マスク言語モデルの源流のひとつはクローズテスト（Cloze test; Taylor, Journalism Quarterly 1953）です。クローズテストは文章の読みやすさを定量化しようという文脈で提唱された読解力の計測法で、「読者の読解力が高ければ一部を黒塗りした文章の復元をできるだろう」という考え方に基づいています（DuBay, 2004, PDF）。穴埋め問題をよく解けるようになった BERT は十分な読解力を手にしたことになるだろう、と期待しているわけです。

サブワード

マスク言語モデルを含めニューラルネットを基盤とする自然言語処理モデルは、最近ではテキストの最小単位として単語ではなく サブワード（subwords）を用いるの主流です。サブワードの「サブ」は「より下位区分の、細かい単位の（sub-）」という意味で、単語よりもさらに短い文字列のことです。サブワードに基づくモデルでは、たとえば「scaling」という単語を「scal + ing」とふたつのサブワードに分割して処理することがあります。

サブワード分割のアルゴリズムとしては Byte Pair Encoding（BPE; Sennrich et al., ACL 2016）、WordPiece（Schuster and Nakajima, ICASSP 2012）、ユニグラムモデル（Kudo, ACL 2018; 工藤, NLP 2018, PDF）が有名です。今では手元の自然言語処理プロジェクトでサブワードを利用するのも非常に簡単で、たとえば SentencePiece や Hugging Face の Transformers ライブラリ に主要なサブワード分割アルゴリズムが実装されています。

サブワードという枠組みにはいくつかの重要なメリットがあります。

一点目は計算コスト上のメリットです。サブワードという枠組みを用いることで、語彙サイズ（“単語” 数）ひいては単語埋め込み行列のサイズを削減でき、ニューラルネットのいわゆるロジット部分の計算コストを削減できます。

もう一点、モデルにとっての未知語（unknown words）が減少するのもサブワード化の大きなメリットです。サブワードには文字の集合 {a, b, c, …, z, , ,. ,…} が含まれており、文字種が極めて多い言語を除いて、ほとんどすべての単語をサブワード列として表現することができます。未知語は自然言語を取り扱う以上は必ず立ちはだかる壁であり、各種モデルの性能低下の一因でした。我々の自然言語は決して整然とした体系ではありません。どんなに巨大な “単語” リストを用意したとしても、新語、固有名詞、専門用語、符牒、くだけた表現など、リストから溢れてしまう単語は無数に存在します。また単語頻度は経験的にべき分布と呼ばれる裾の重い分布に従うことが知られています。これは、コーパスサイズを少し大きくすれば必ずそれまで登場しなかった単語が簡単に現れることを意味します。Google や Meta（Facebook）等の巨大テック企業が尋常ならざるサイズのコーパスを用いて単語リストを作ったとしても、テスト時には必ず見たことのない単語が登場する、というのが未知語の問題です。

サブワードは、語彙サイズを制限しつつ未知語の問題を回避できるという点で今日の自然言語処理に欠かせない重要な枠組みです。仮に将来ニューラルネットや誤差逆伝播法が廃れたとしても、サブワードのメリットは継続的に評価され続けるでしょう。

問題意識：いつもひとかたまりで登場する句がマスク言語モデルを “甘やかしている” のでは

さて、マスク言語モデルとサブワードを紹介したところで本題に入りましょう。

今回紹介する ICLR 2021 の論文 “PMI-Masking: Principled masking of correlated spans” は、BERT などに課せられる穴埋め問題の中に極端に簡単な出題が含まれているのではないかという仮説からはじまります。

サブワードの場合

たとえば「2050年12月に衆参両院の本会議で行われた総理大臣指名選挙で自然言語花子氏が第150代の内閣■■大臣に選出された。」という穴埋め問題を検討しましょう。日本語話者の直感からすれば、周辺文脈を全く参照せずとも「内閣■■大臣」の部分だけで解けてしまう簡単な問題に見えるでしょう。

論文では「e_[mask]_val_ue」という例が取り上げられています。 こちらも eigenvalue（固有値）という単語を知っている人であれば、周辺文脈を全く参照せずととも「e_[mask]_val_ue」の部分だけで穴埋めできてしまいそうです。BERT にこうした簡単すぎる問題を与えると BERT は文脈を見ずに近傍のトークンという抜け道を使って問題を解いてしまうのではないか？ 結果として言語モデルとしてうまく育たないのではないか？ 著者らはこの甘やかし仮説でこの論文をはじめています。

「簡単すぎる問題を与えると BERT は成長しないだろう」はこの段階では仮説に過ぎません。実際のところ「内閣■■大臣」や「e_[mask]_val_ue」のような簡単そうな穴埋め問題、つまりもともと1単語だったサブワード列の一部だけをマスクした練習問題は、本当に BERT を「甘やかして」いるのでしょうか？著者らは面白い予備実験を通して甘やかし仮説を裏付ける経験的な証拠を与えています。

予備実験では2つのマスク戦略（甘やかし具合）と3つの語彙サイズ（サブワード分割の細かさ）を組み合わせて BERT の事前訓練がおこなわれます。

  • 2つのマスク戦略
    • Random Masking 戦略 ：もともと1単語だったかどうかは気にせずランダムにサブワードを黒塗りする。「e_[mask]_val_ue」のような簡単な穴埋め問題が生じうる（BERT の元論文の3.1節での提案）。
    • Whole Word Masking 戦略 ：もともと1単語だったサブワード列はかならずまとめて黒塗りする。「e_[mask]_val_ue」のような簡単な穴埋め問題は生じえない（BERT の GitHub リポジトリ に2019年5月に追記）。
  • 3つの語彙サイズ
    • 30k
    • 20k
    • 10k
    • ※ 語彙サイズが小さくなるほどリストに登録できる単語が少なくなり、「eigenvalue」→「e_[mask]_val_ue」のように単語がサブワードに分割されるケースが増えます。

結果は 図1 の通りです。


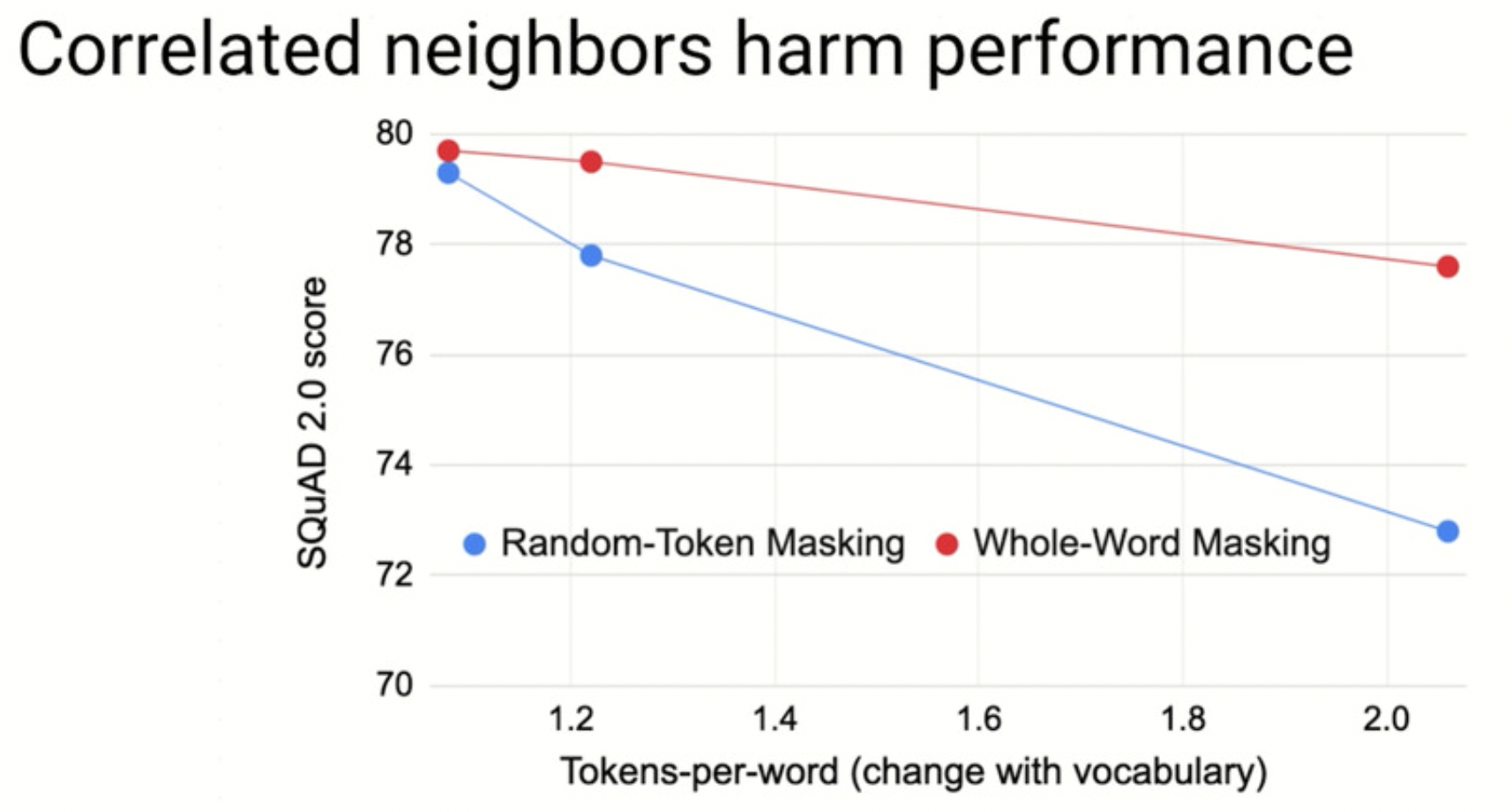
図1：著者スライドより抜粋。

Random Masking 戦略（青色）をとると、語彙サイズが小さくなるにつれて（x軸が大きくなるにつれて）「e_[mask]_val_ue」のような簡単すぎる問題がたくさん出現されることになります。そしてこのときたしかに後段タスクでの性能（y軸）は確かに大きく劣化することがわかります。

一方で、Whole Word Masking 戦略（赤色）をとる場合、語彙サイズが小さくなったとしても（x軸が大きくなったとしても）「e_[mask]_val_ue」のような簡単すぎる問題が出題されません。そしてこのとき、後段タスクでの性能（y軸）の劣化の度合いは Random Masking 戦略に対してかなり小さいことが見てとれます。

以上の予備実験から、周辺文脈から解けてしまう簡単な穴埋め問題を渡して BERT に「楽をさせ」ることで BERT の万能テキストエンコーダとしての性能が劣化することが強く示唆されます。

単語の場合

同様の問題はサブワード列だけではなく単語列でも起きることが容易に予想されます。

たとえば「常軌を逸する」「顰蹙を買う」といった言い回しを知っている日本語ネイティブにとって、「常軌を■■」「顰蹙を■■」はその周辺文脈を全く参照せずに解けてしまう簡単な穴埋め問題に見えるでしょう。英語にも “editor in chief”（編集長）、“carbon footprint”（炭素排出量）、“as far as”（〜の限り）などこうした定型句がたくさん存在します。こうした「ひとかたまりで登場しやすい単語列」のことを 連語（collocations）とか 複単語表現（multi-word expressions）と呼びます。

サブワードでの予備実験を踏まえれば、単語の場合もこうしたひとかたまりの系列をまとめてマスクすることで BERT の甘やかしを軽減できそうです。しかし、「元が1単語だった」という簡単な判定法を持ち込めるサブワード列とは異なり、単語列の場合はどの部分がひとかたまりかを判定する基準が非自明です。

「ひとかたまり」の同定：自己相互情報量を3語以上に拡張

著者らは自己相互情報量を拡張することでひとかたまりの句を同定します。

自己相互情報量

連続する2単語、たとえば “New York” という単語列の共起の強さ（同時に出現しやすさ、連語である度合い）は様々な方法で測定することができます。
自然言語処理でとくによく用いられるのは 自己相互情報量（Pointwise Mutual Information; PMI; Church and Hanks, Computational Linguistics 1990）です。ふたつの単語 $w_1$ と $w_2$ の PMI は各単語の出現確率を用いて次のように計算されます。

$$
\mathrm{PMI}(w_1,w_2) = \log \frac{p(w_1,w_2)}{p(w_1, \cdot)p(\cdot, w_2)}\text{.} \qquad \text{(1)}
$$

右辺分母の $p(w_1,\cdot)$ と $p(\cdot,w_2)$ は、「適当に連続する2単語を持ってきたときに1単語目が $w_1$ である確率」「適当に連続する2単語を持ってきたときに2単語目が $w_1$ である確率」です。かけあわせた $p(w_1,\cdot) p(\cdot,w_2)$ はいわゆるチャンスレベルで、「$w_1$ と $w_2$ が 仮に無関係であれば、適当に連続する2単語を持ってきたときに $w_1 w_2$ という単語列である確率はこの程度でしょう」という値です。一方分子 $p(w_1, w_2)$ は「 実際に コーパスから連続する2単語を拾ってきたときに $w_1 w_2$ である確率」です。PMI が大きいとき、つまりチャンスレベルよりも実際に出現する確率が大きいとき、$w_1 w_2$ という単語列は繋がりのよい句であると判断できます。

ここで $\mathrm{PMI}(w_1,w_2)$ と頻度 $p(w_1,w_2)$ は全く異なる性質を持つことに注意しておきます。頻度はたくさん出てくる単語列を常に高く評価しますが、PMI はそうではありません。論文では “book is”（本は…）と “boolean algebra”（ブール代数）という2つの単語列を例にあげ PMI の良さを説明しています。“book is” は多くの文書に頻繁に現れる単語列です。Wikipedia と BookCorpus（著名な書籍コーパス）には合わせて34,772回も現れるそうです。“boolean algebra” はほとんどの文書に登場しない単語列で、同コーパスには合わせて849回しか現れないそうです。つまり、頻度で測れば “book is” が “boolean algebra” よりも高く評価されます。一方で PMI を見ると話は大きく変わります。“book is” の PMI は全「2単語列」の中で760,000位、“boolean algebra” は16,000位とのことで、順位は逆転します。

「繋がりの良い単語列を知りたい」「一部を見れば残りを簡単に予測できてしまうような単語列を知りたい」という目的に照らせば、“boolean algebra” の方を “book is” よりも高く評価する PMI の方が適切なことがわかるでしょう。いくら “book is” が高頻度に登場するとは言え、「[mask] is」という穴埋め問題をこの局所的な情報だけから高い正解率で解くのはほとんど不可能だと思われますね。

ナイーヴな拡張

PMI は便利な道具ですが、2単語の場合にしか適用できないことが今回の場合は力不足です。「e_igen_val_ue」が4つのサブワードで構成されていたのと同様、共起しやすい単語列の長さも2とは限りません。日本語であれば「かも_しれ_ない」「感染_拡大_対策」「所_に_より_雨_で_しょう」などはいかにも簡単すぎる練習問題を生み出しそうです。英語であれば “United States federal courts”（アメリカ合衆国連邦裁判所）、“the pot calling the kettle black”（五十歩百歩）、などやはり枚挙にいとまがありません。「枚挙にいとまがない」も簡単な練習問題を生み出しそうですね。

そこで3単語以上に適用できるよう PMI を拡張しようとすると、素直には次の形式になりそうです（Van de Cruys, workshop 2011）。

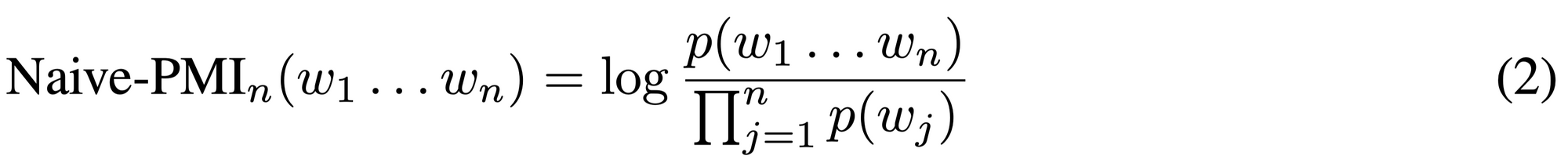
この式も、PMI と同様に、各単語の出現確率の積（分母、チャンスレベル）と実際に単語列が現れる確率（分子）の比を計算しています。

ところがこの形式は、共起しやすい単語列を内側に含むような単語列に高い値を割り当ててしまう、という欠点があります。

具体例から見てみましょう。“Kuala Lumpur”（クアラルンプール；マレーシアの首都）はいかにも共起しやすい単語列で、実際に高い PMI を持ちます。一方で “Kuala Lumpur is”（クアラルンプールは…）という3単語からなる単語列は、“book is” と同様の理由で「ひとかたまり」だとは考えたくありません。式 (2) で与えられる自然な拡張は、残念ながら、“Kuala Lumpur is” のような単語列を “editor in chief”（編集長）のような連語よりも高く評価してしまいます。

興味がある人向けに式でもこれを説明します。素直な PMI 拡張を次のように変形すると（元論文4ページ）、

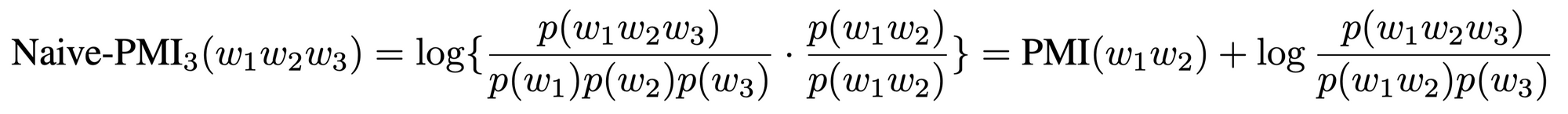
  • $\mathrm{PMI}(\text{“Kuala”}, \text{“Lumpur”})$ が大きければ（“Kuala” と “Lumpur” が共起しやすければ）、
  • $\displaystyle \log\frac{p(\text{“Kuala Lumpur”}, \text{“is”})}{p(\text{“Kuala Lumpur”})p(\text{“is”})} = \mathrm{PMI}(\text{“Kuala Lumpur”}, \text{“is”})$ ほぼ $0$ でも（“Kuala Lumpur” と “is” の共起の強さがチャンスレベル程度であっても）、
  • 左辺の $\text{Naive-PMI}(\text{“Kuala”}, \text{“Lumpur”}, \text{“is”})$ には高い値が割り当てられる

ことがわかります。

提案する拡張

著者らはナイーヴな PMI 拡張の欠点を解消するため新しい PMI 拡張を提案します。

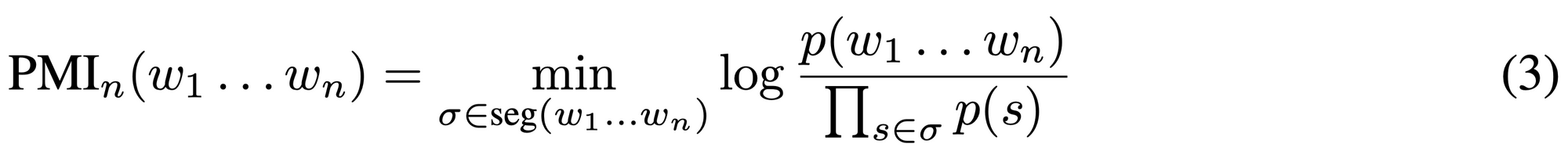
この尺度は直感的には「単語列全体での共起の強さは、一番繋がりの弱い “接続箇所” が支配すると思いましょう」というものです。“Kuala Lumpur is” であれば、“Kuala Lumpur” と “is” の間の繋がりは弱く、結果として提案尺度は “Kuala Lumpur is” に小さな値を割り当てることになります。

興味があるかた向けに式でも説明します。まず式 (2) の $\mathrm{seg}(w_1\dots w_n)$ は与えられた単語列のすべての分割を表します。たとえば “Kuala Lumpur is” という3単語からなる文字列は、

$$
\mathrm{seg}(\text{“Kuala Lumpur is”}) = \lbrace\lbrace\text{“Kuala”}, \text{“Lumpur”}, \text{“is”}\rbrace, \lbrace\text{“Kuala Lumpur”}, \text{“is”}\rbrace, \lbrace\text{“Kuala”}, \text{“Lumpur is”}\rbrace\rbrace
$$

と3通りの分割が可能です。

「$\min$」が意味しているのは、「単語列全体での共起の強さは 一番 繋がりの弱い分割における繋がりの強さとしましょう」の「一番」の部分です。“Kuala Lumpur is” であれば、分割 $\lbrace\text{“Kuala Lumpur”}, \text{“is”}\rbrace$ から出てくる項 $\log \frac{p(\text{“Kuala Lumpur is”)}}{p(\text{“Kuala Lumpur”})p(\text{“is”})} = \mathrm{PMI}(\text{“Kuala Lumpur”}, \text{“is”})$ が小さい値を持つことで $\min$ 全体が小さくなります。

実際、ナイーヴな PMI で得られていた

$$
\text{Naive-PMI}_3(\text{“Kuala Lumpur is”}) > \text{Naive-PMI}_3(\text{“editor in chief”})
$$

という望ましくない評価は、提案法によって

$$
\mathrm{PMI}_3(\text{“Kuala Lumpur is”}) < \mathrm{PMI}_3(\text{“editor in chief”})
$$

と解決するそうです。

【分割の仕方に関する補足】

なおここで、分割の集合 $\mathrm{seg}(w_1\dots w_n)$ は、「何も分割しない」という分割は含みません。つまり分割 $\mathrm{seg}(\text{“Kuala Lumpur is”})$ は $\lbrace\text{“Kuala Lumpur is”}\rbrace$ を含みません。

この制約は、次のように考えれば自然です。まず我々は、分子（実際の共起）$>$ 分母（チャンスレベル）になるようなパターン、つまり $\min$ の中が正の値になるような共起しやすい句を探したかったわけです。ところが自明な分割は $\log \frac{p(w_1\dots w_n)}{p(w_1\dots w_n)} = 0$ から $\min$ の中身に $0$ を入れることになり、「分子 $>$ 分母」になるような共起しやすいパターンをすべて上書きしてしまいます。

※ $\mathrm{seg}(\cdot)$ が自明な分割を含まないことは論文内の “(excluding the identity segmentation)” という記載から読み取ることができます。

実験

最後は効果検証です。「ひとかたまりの単語列をまとめてマスクして BERT を甘やかさないことで言語モデルはよりよく成長させることができる」という仮説は実際のモデルでも成り立つのでしょうか？

著者らは、2つの実験を通してこの仮説に肯定的な証拠を与えています。さらに、提案法によって事前訓練自体が確かに「難しく」なったかどうかについても確認し、こちらも肯定的な証拠を与えています。

提案法の設定

実際にマスクされる連語は次の方法で決定されます。

  1. 訓練コーパス中に10回以上出現する 2-gram（2単語列）, …, 5-gram を連語候補として取り出す
  2. それぞれの句に対して提案法 $\mathrm{PMI}_n$ で「ひとかたまり度合い」を計算し、上位 800,000 件を取り出す

著者らはこの「800,000」という数字を決めるために地道で説得的な準備をしています。まず、連語候補のごく一部に対して、それが本当に連語・複単語表現かどうかを人手でアノテーションしています。たとえば “edior in chief” は連語だが “Kuala Lumpur is” は連語ではない、という具合です。日本語であれば、「内閣総理大臣」は連語だが「感染対策を」は連語でなない、という具合です。次に、「スコア上位何件かの連語を取り出す」という行為によって連語候補を正例負例に分類すると考えたときに適合率（precision）と再現率（recall）のバランスが取れるように、つまり $F_1$ スコアが最良となるように上位何件を使うか決めています。以上の手順で見つけたスイートスポットが 800,000 だったということです。

※ ここで述べた手順は4.1節「Experimental Setup」ではなく3.2.1節「PMI-Masking」および付録A「Determining the masking vocabulary size」に記載されています。

※ 適合率、再現率、$F$値（F-measure）等、ランキング問題や情報検索に用いられる評価尺度については、英語版 Wikipedia 記事、酒井『情報アクセス評価方法論』(2015) などを参照してください。

【提案法を活用するための注意点】

注意点として、我々読者がこの論文の提案法を活用したい場合は次の2点に気をつける必要があります。

まず 800,000 という値をそのまま使うことはできません。この値は著者らが用いたコーパス、すなわち英語版の Wikipedia + BookCorpus という特定のコーパスに依存することが容易に予想できるからです。極端な例として、ツイート1つからなる非常に小さい “コーパス” が 800,000 もの連語を含むことはあり得ませんね。

また予備実験（元論文の付録A）によれば、$F_1$ スコアは連語リストのサイズに対してそれなりに鋭敏で、0.3程度〜0.7程度と広い範囲の値をとっています。これは、適当に連語リストのサイズを決めてしまうと、人間のアノテーションとはかなりギャップのある “連語” リストができることを意味しています。

以上から、読者が著者とは異なるコーパスで BERT を事前訓練したい場合は、著者同様小規模なアノテーションの上でチューニングするか、コーパスサイズに比例した値を採用するなどのやり方が考えられます。特に前者の場合はある程度のコストがかかりそうです。多少小規模であっても既存の連語リストを用いるのも選択肢かもしれません。

もう1点気をつけるべき点として、2-gram から 5-gram までそれぞれで作ったリストの統合の仕方が不明です。

著者らも3.2.1節で指摘しているように $\mathrm{PMI}_n$ スコアは句の長さ $n$ に鋭敏です。すなわち $n$ が異なるような $\mathrm{PMI}_n$ 同士は直接比較できず、連語リストのサイズは本来トークン数 $n$ 毎に決める必要があるはずです。我々読者ができる将来の研究として、異なる $n$ の $\mathrm{PMI}_n$ 同士を直接比較できるような手法を作れればコミュニティにとってありがたい仕事となるでしょう。たとえば Normalized PMI（Bouma, GSCL 2009, PDF）をうまく拡張して提案法の値域を $[0,1]$ に絞るなどの方法が考えられそうです。

訓練効率

ひとつめの実験では、提案法によって訓練効率がどの程度改善するかを確認しています。


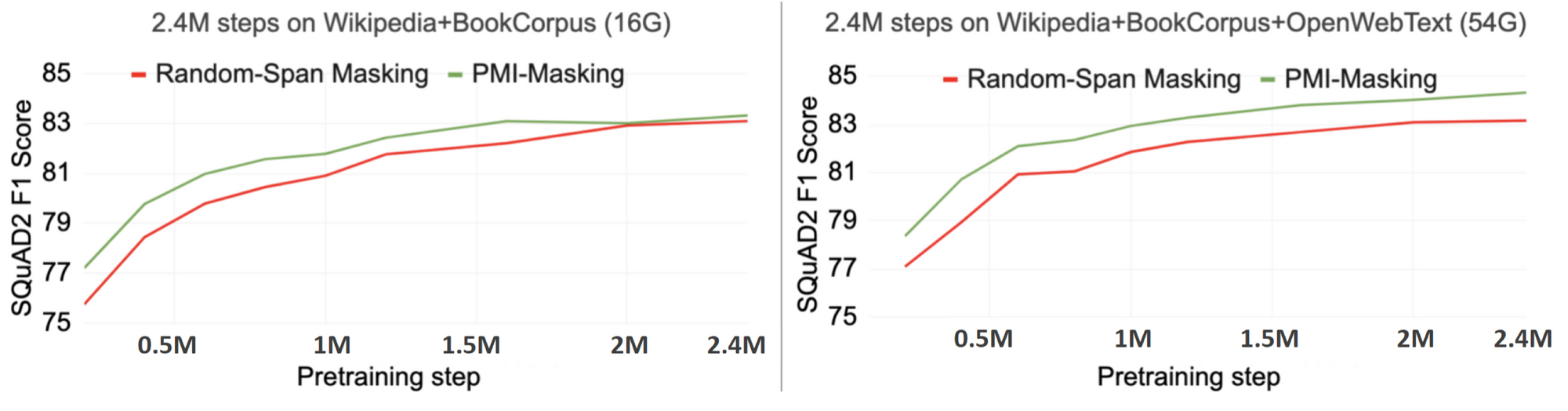
図2：元論文の Figure 2

図2 は左右とも緑色が提案法、赤色はベースラインです。赤色のベースライン（Joshi et al., TACL 2020）も連続するトークンをまとめてマスクするという点では提案法と同じですが、共起しやすいスパンではなくランダムなスパンをマスクします。横軸は事前訓練のステップ数を、縦軸は事前訓練後に SQuAD 2.0 （Rajpurkar et al., ACL 2018）という著名な質問応答タスクを解いたときの性能を表しています。

図2の左図 を見てください。提案法（緑色）は既存法（赤色）のおよそ半分の訓練時間で、後段タスクの性能という意味で既存法と同様の品質に達することがわかります。簡単な練習問題を提供せず BERT を「甘やかさない」ことで事前訓練がむしろより効率的に進むことを意味します。そしてこの高効率は、単に連続トークンをマスクするだけでは得られないことがわかります。

次に 図2の右図 を見てください。左図とはコーパスサイズだけが異なり、右図ではずっと大きなコーパスでモデルが訓練されています。こちらの設定だと、提案法（緑色）は左図では存在していた「性能の壁」を突破しています。連語をまとめてマスクするという提案訓練戦略はコーパスサイズが大きい場合により強い優位性を持つことがわかります。

一点注意点として、ここで示された「訓練時間」には連語を決定する時間は含まれていません。あくまでも実際の事前訓練にかかる時間のみを計測しています。

後段タスクでの性能

ふたつめの実験では、より広範なベースライン手法と比較して提案法の後段タスク（RACE, Lai et al., EMNLP 2017）の性能面での優位性を確認しています。結果は「各種強力な先行モデルたちよりも強かった」です。詳細が気になるかたのために以下に簡単な説明をつけます。


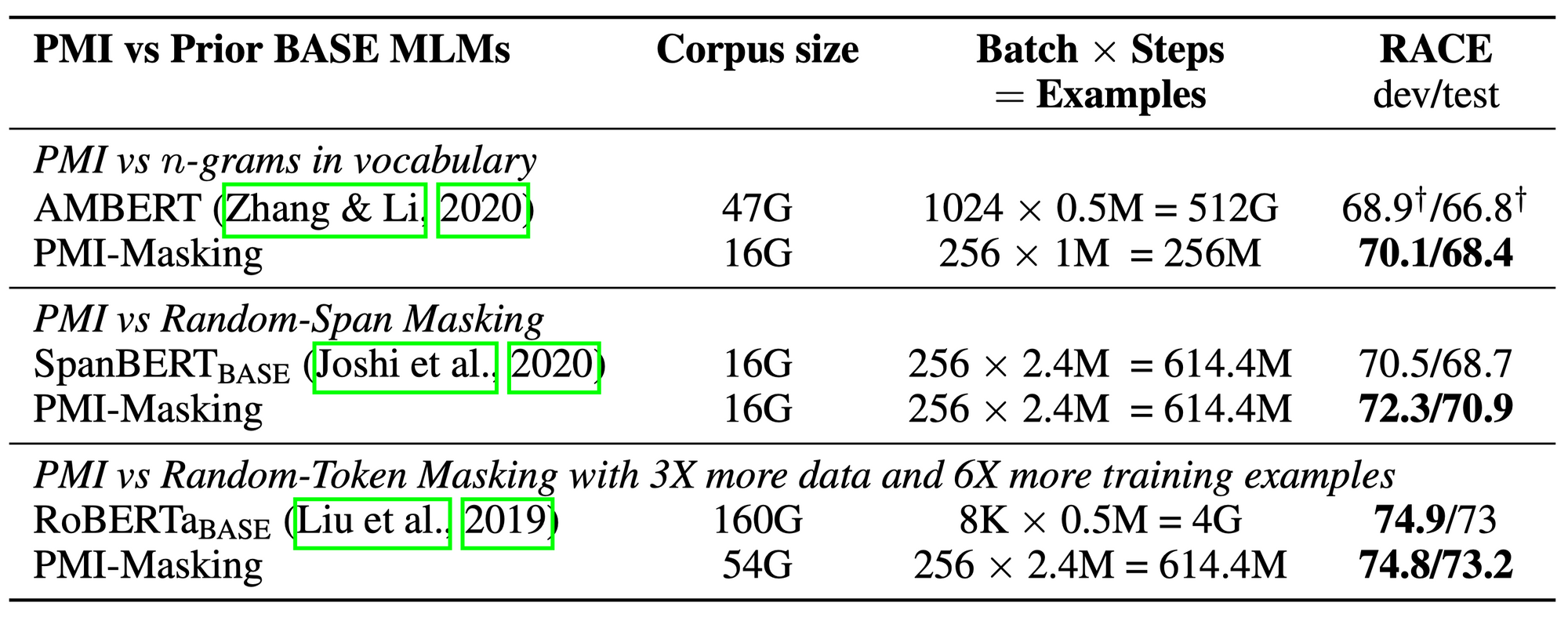
表1：元論文の Table 3

上段の AMBERT （Zhang et al., Findings of ACL 2021）は $n$-gram 自体を語彙に入れるモデルです。たとえば “Kuala Lumpur” を「単語」として語彙リストに入れてしまいます。

中段の SpanBERT （Joshi et al., TACL 2020）は Random Span Masking（連語とは限らない適当な連続トークンをマスク）によって簡単な練習問題を一定程度回避します。

提案法、つまり連語に対してマスクをおこなうという訓練戦略は、これらの戦略をとるよりも後段タスクでの良好な結果につながることがわかります。ただし手法毎に変化しているパラメータは $n$-gram の扱い方だけではなく、完全な対照実験にはなっていないことに注意してください。

RoBERTa （Liu et al., arXiv 2019）は BERT ファミリーの中でもとりわけ “強い” モデルとして知られています。また RoBERTa は提案法に対して3倍程度のサイズのコーパス、6倍程度の練習問題数で訓練されています。ただし事前訓練におけるマスクのしかたはランダム、つまり簡単すぎる練習問題が出題され得る設定です。

提案法は驚くべきことに大きなコーパスで訓練した RoBERTa と後段タスクの性能でほとんど並びます。連語の単位でマスクするという基本戦略の有用性を強く示唆する結果と言えます。

訓練誤差

みっつめの実験では、提案法の出題する穴埋め問題が BERT にとって “難し” かったかを確かめています。論文内での扱いは小さいですが、マスク穴埋めによる事前訓練 → 微調整という現代自然言語処理の基本パラダイムへの示唆を与えるという点で重要な実験だと考えています。


表2：元論文の Table 4

表2 では、各マスク戦略での事前訓練の結果、最終的にマスク穴埋めの誤差がどこまで小さくなるのかが示されています。評価尺度はトークン単位のパープレキシティ（perplexity）で、値が小さければモデルが穴埋め問題をよく解けていることを意味します。数値を見てみると、表の最上段の Random Masking 戦略から最下段の提案法に向かうにつれて穴埋め問題の最終的な正解率が低くなることがわかります。提案法によって確かに簡単すぎる練習問題が減り、訓練後ですら与えた難問たちを解ききれていないことがわかります。

【穴埋めによる事前訓練 → 微調整 パラダイムへの示唆】

この訓練誤差の値と後段タスクにおける性能（表3）とを比べてみると、驚くべきことにちょうど逆の傾向を示していることがわかります。さまざまな穴埋め戦略でモデルを訓練してみると、訓練誤差の小ささ（うまく穴埋め問題を解けたかどうか）と後段タスクの性能に逆相関が見られる、ということです。モデルが練習問題を十分に解けなかったとしても、いやむしろ十分に解けない方が後段タスクでは性能を発揮するということです。


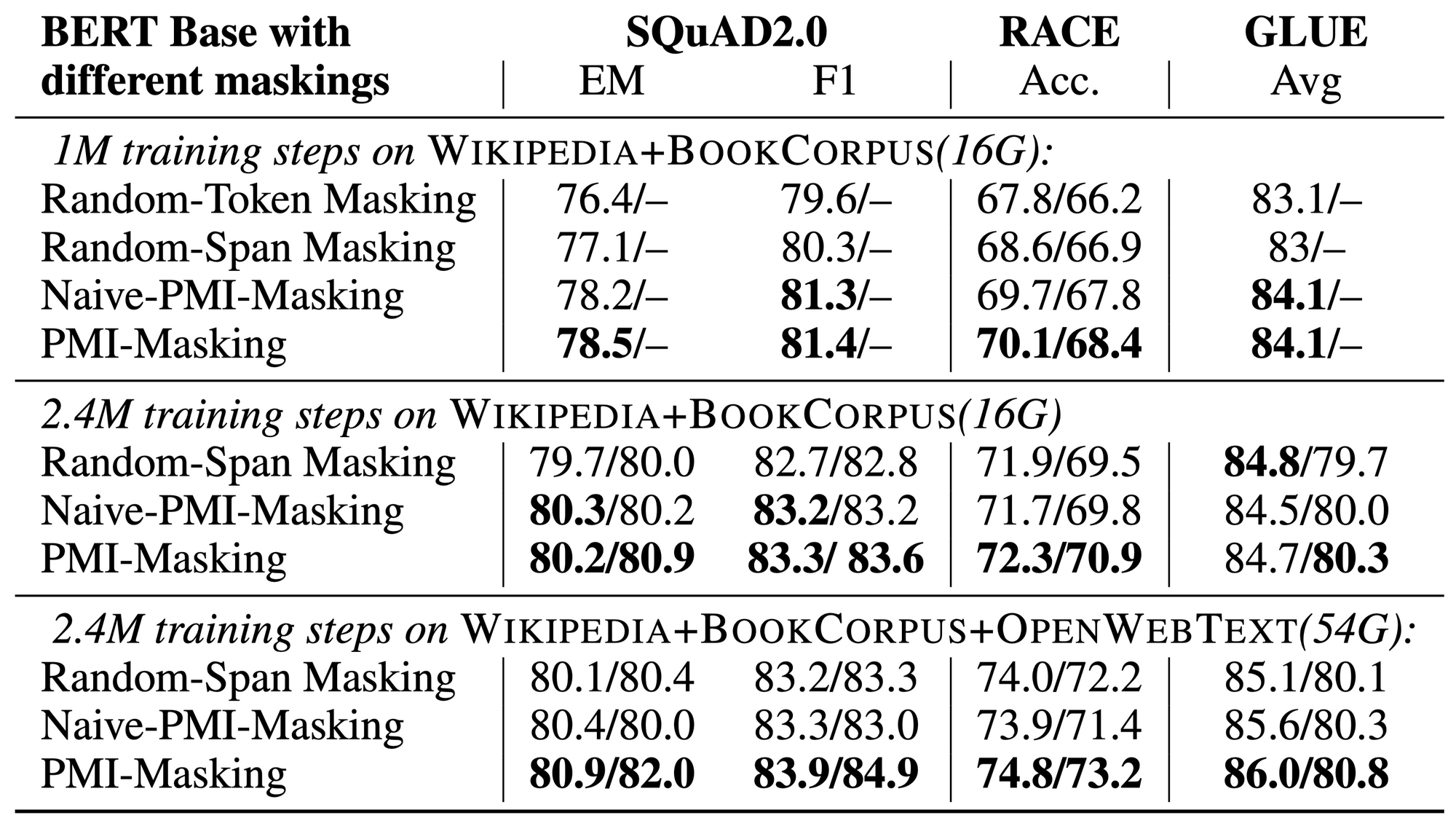
表3：元論文の Table 2

マスク言語モデルは広範な自然言語処理タスクに対して飛躍的性能向上をもたらしました。またその力の源泉はマスク穴埋めという事前訓練戦略にあると考えられていました。つまり、モデルが穴埋め問題が解けるようになる ＝ モデルがある程度テキストを “読解” できるようになる ＝ モデルが後段タスクで性能を発揮する、と考えられていました。

ところが上のふたつの表は、モデルがマスク穴埋めに成功することと後段タスクでの性能向上は純粋な正の相関関係ではないことを示しています。この研究をきっかけに、万能テキストエンコーダーをいかに訓練すべきか、いかなる問題を与えるべきか、テキストをどういった表現を与えるべきかという難題への人類の理解が進み、表現学習がさらに深化することを期待しています。

まとめ

まとめです。

マスク言語モデルの事前訓練で出題される問題の中には「顰蹙を■■」や「New [mask] Yankees」のようにごく近傍を見れば解けてしまう簡単な問題が含まれ得ます。今回紹介した ICLR 2021 の論文 “PMI-Masking: Principled masking of correlated spans” では、3トークン以上からなる句の「連語度合い」を測れるよう自己相互情報量を拡張し、こうして推定した連語をまとめてマスクする「甘やかさない」訓練戦略を提案しました。実験の結果、事前訓練の効率が高まり、また後段タスクにおける性能も向上することがわかりました。

論文のとくに良い点として、個々の仮説検証が丁寧で説得的であることが挙げられます。

たとえば「簡単すぎる練習問題は訓練に悪影響なのでは？」という仮説を検証するために、著者らはサブワード単位でマスク戦略と語彙サイズを組みあせた予備実験をおこないました（図1）。最小のコストで仮説の妥当性を示す大変良いデザインの予備実験と言えるでしょう。また、PMI を拡張する提案法は、難しい練習問題を出せば言語モデルはよく育つはずだという仮説を検証するための中間的な道具に過ぎません。提案法で作った練習問題が確かにモデルにとって難しかったことをパープレキシティを通して直接的に確認した実験（表2）は、論文全体の仮説検証の筋を一本通すという意味で重要です。

これら、小さく簡単にもかかわらず議論上大きな役割を持つ実験は、著者らが仮説自体を十分に議論・言語化したあとに手を動かしたからこそおこなえたものでしょう。研究プロセス自体の好例だと考えます。また個人的に後者の練習問題の難易度を確認した実験は、マスク穴埋めによる事前訓練 → 微調整という現代自然言語処理の基本パラダイムへ示唆を与えるという点でも論文の価値を高めていると考えます。

論文の欠点・限界として連語決定のプロセスがまだこなれきっていないことが挙げられます。

PMI の拡張手法自体は便利に見えまた魅力的ですが、異なる長さのスパンの共起の強さを比べられないことと、良い辞書サイズの決定にアノテーションが伴うことは、それぞれ再現実験をする上で壁になるでしょう。また、提案法はこの連語の同定を追加コストとして支払っており、モデルの事前訓練時間のみを比較して提案法は先行手法より効率的だと述べている5.2節はやや過大申告です。

とはいえこれらの欠点は論文全体の魅力に比べれば十分に小さく、人工知能周辺でもっとも競争的な会議のひとつである ICLR に Spotlight 枠で採択されたことは十分に妥当だと考えます。

謝辞

もしこの記事が魅力的な観点で論文を紹介できているとしたらひとえに広義同僚のみなさんとの日々の議論のおかげです。

この論文の紹介にあたっては、とりわけ東北大学乾研究室および鈴木研究室の関係者のみなさん、特に小林颯介さん（PFN）；有志研究会Deep神保町のみなさん；論文読み会最先端NLP勉強会2021の参加者のみなさん、との議論の機会に感謝したいです。

記事に誤りが含まれていた場合は筆者の問題です。忌憚のないフィードバックをお寄せください：yokoi@tohoku.ac.jp

文責：横井祥（東北大学）

関連記事

最新研究から学ぶ 言語モデルの性能を向上させる5つの簡単なトリック
最近になって、言語モデルの性能を向上させる最新の研究が立て続けに発表されています。いずれも、比較的簡単な工夫で、トランスフォーマー・ベースの言語モデルの性能を改善したり、訓練を効率化したりといったことを可能にするものが多く、「GPT-3 超え」を達成したものもあれば、我々の日々の業務にも応用できそうなアイデアも多くあります。本記事では、最近の「言語モデルの性能向上テクニック」に関する文献をまとめて紹介します。
ステート・オブ・AI ガイド萩原 正人
BERTとトランスフォーマーはこう使え　「効果的な訓練・微調整のコツ」総まとめ
BERTやトランスフォーマーを使った自然言語処理が普及していますが、これらのモデルを効果的に訓練・微調整をするためには未だに「職人芸」的なテクニックが必要となります。「これを知っているだけで BERT とトランスフォーマーの訓練・微調整が劇的に安定・改善する」という手法を比較・検討した論文が最近になっていくつか出てきましたので、まとめて解説したいと思います。
ステート・オブ・AI ガイド萩原 正人